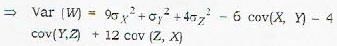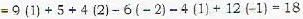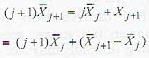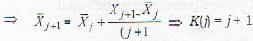Test: Probability and Statistics - 1 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Probability and Statistics - 1
Consider the experiment of throwing two fair dice. What is the probability that the sum of the numbers obtained in these dice is even?
Two dice are rolled until the sum of the numbers appearing on these dice is either 7 or 8. What is the probability that the sum is 7?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A pair of unbiased dice is rolled together till a sum of either 5 or 7 is obtained. The probability that 5 comes before 7 is.
A letter is taken at random from the letters of the word ‘STATISTICS ’ and an other letter is taken at random from the letters of the word ‘ASSISTANT’. The probability that, they are the same letter is .
A bag contains 6 red and 4 green balls. A fair dice is rolled and a number of balls equal to that appearing on the dice is chosen from the urn at random. The probability that all the balls selected are red is.
A six faced die is a biased one. it is thrice more likely to show an odd number than to show an even number. It is thrown twice. The probability that the sum of the numbers in the two throws is even, is.
A letter is knwon to have come from either TATANAGAR' or CALCUTTA. On the envelope, Just two consecutive letters, TA, are visible. The probability that the letter has come from CALCUTTA is.
A card is drawn from a pack. The card is replaced and the pack is reshuffled. If this is done six times, the probability that 2 hearts, 2 diamonds and 2 club cards are drawn is.
There are three piles of identical yellow, black and green balls and each pile contains at least 20 balls. The number of ways of selecting 20 balls if the number of black balls to be selected is twice the number of yellow balls is.
Two balls are drawn at random from a bag containing 6 white, 4 red and 5 black balls. The probability that both these balls are black, is :
Let X be the random variable giving the number of heads obtained in 162 successive tosses of a biased coin with probability of getting head in a toss is 1/3. Assume that the losses are in dependent. The standard deviation of X is.
Assume that the number of buses arriving at a bus-stop in an interval of t minutes is poisson distributed with parameter 0.21. The probability that at least three buses will arrive during a 10 minute interval is.
The standard deviation of first, n natural numbers is :
Of a distribution, coefficient of skewness is 0.32, standard deviation is 6.5 and the mean is 29.6 then its mode will be :
A ship arrives at a port and 40 sailors on board go ashore for revelry. Later at night, the 40 sailors return to the ship and in their state of inebriation, each chooses a random cabin to sleep in. What is the expected number of sailors sleeping in their own cabin?
Suppose there are 15 different types of coupons and suppose that each time one obtains a coupon, it is equally likely to be any one of the 15 types. The expected number of different types that are contained in the set of 5 coupons is
The joint density of X and Y is given by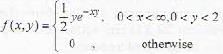 The value of E|X/2|Y = 1 is equal to
The value of E|X/2|Y = 1 is equal to
A and B throw with one die for a stake of Rs 11 which is to be won by the player who first throws 6. If A has the first throw, what is the expectation of his winning the stake?
If the random variables X, Y and Z have the means μx = 2, μy= -3 and μz = 2, the variances 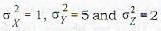 and covariances cov(X,Y) = -2, cov(X, Z) = -1 and cov (Y, Z) = 1, the variance of W = 3X - Y+ 2Z is
and covariances cov(X,Y) = -2, cov(X, Z) = -1 and cov (Y, Z) = 1, the variance of W = 3X - Y+ 2Z is
A computationally efficient way to compute the sample mean of the data x1,x2,...xn is as follows:
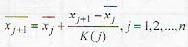
Then K(j) is equal to
|
27 docs|150 tests
|


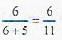
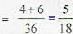
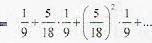
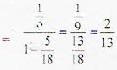

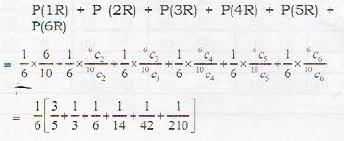
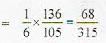
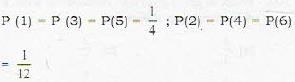
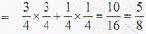
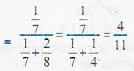
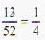
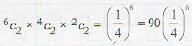
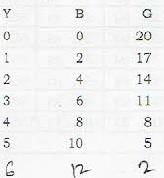
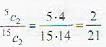
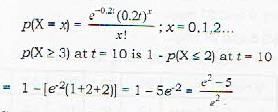
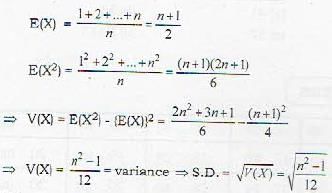

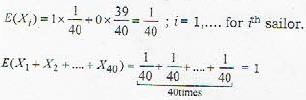
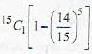
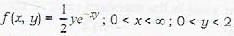
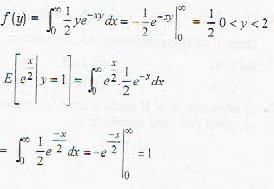

 [sum of infinite terms of G.P.]
[sum of infinite terms of G.P.]