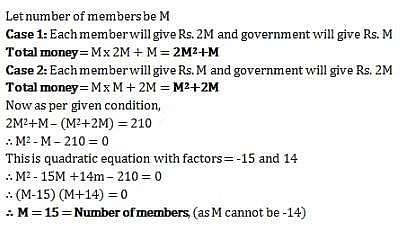Test: Problem Solving- 1 - SSC CGL MCQ
10 Questions MCQ Test SSC CGL Tier 2 - Study Material, Online Tests, Previous Year - Test: Problem Solving- 1
If the product of two integers x and y is less than 82 with y being a multiple of three. What is the highest value that x may have?
Adam is 2 years older than Mike. The square of Adam’s age is 28 greater than the square of Mike’s age in years. What is the sum of Adam’s age and Mike’s age?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Adam has bought a certain number of apples. Jen has bought 5 times the fruit that Adam has bought. If Jen has bought two and a half dozen apples how many apples does Adam have?
What could be the possible value of 'y' after the intersection of points
y= -x2 + 3 and y= x2- 5
A house is built by 20 workers in 30 days. How many workers will be needed to complete the work in 15 days?
Alan has two more than twice as many chocolates as does Alice, and half as many chocolates as does Nadia. If Alice has ‘a’ number of chocolates, then in terms of ‘a’, how many chocolates do Alan, Alice and Nadia have?
Master Chef Alan makes a dish every day from one of his recipe books. He has written 3 books and each book contains 15 different recipes. What is the probability that he will cook 4th dish from 3rd book today?
Milk needs to be thinned to a ratio of 3 parts milk to 2 parts water. The milk-man has by mistake added water so that he has 8 liters of milk which is half water and half milk. What must he add to make the proportions of the mixture correct?
In a Christmas sale, the prices of Dell Laptops were reduced by 10% for public. However, for Dell employees, the price was further reduced by 5%. If the original price of a laptop was $330 before Christmas sale, approximately how much would it cost in a Christmas sale to a Dell employee?
A group wanted to renovate their club. Each member contributed an amount equal to twice the number of members in the club. But the government contributed same amount as the number of members. If each member had contributed the same amount as the number of members and the government had given an amount twice the number of members, then they would have Rs. 210 less. How many members are there?
|
1365 videos|1312 docs|1010 tests
|
|
1365 videos|1312 docs|1010 tests
|