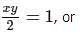Test: Problem Solving- 1 - GRE MCQ
15 Questions MCQ Test Section-wise Tests for GRE - Test: Problem Solving- 1
Each of 100 balls has an integer value from 1 to 8, inclusive, painted on the surface. The number Nx of balls representing integer x is defined by the formula Nx = 18-(x-4)2
What is the interquartile range of the 100 integers?
A “Sophie Germain” prime is any positive prime number p for which 2p + 1 is also prime. The product of all the possible units digits of Sophie Germain primes greater than 5 is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
In a certain game, a large bag is filled with blue, green, purple and red chips worth 1, 5, x and 11 points each, respectively. The purple chips are worth more than the green chips, but less than the red chips. A certain number of chips are then selected from the bag. If the product of the point values of the selected chips is 88,000, how many purple chips were selected?
A manufacturer can save X dollars per unit in production costs by overproducing in certain seasons. If storage costs for the excess are y dollars per unit per day ( X > Y), which of the following expresses the maximum number of days that n excess units can be stored before the storage costs exceed the savings on the excess units?
When the integer x is divided by the integer y, the remainder is 60. Which of the following is a possible value of the quotient x/y?
I. 15.15
II. 18.16
III. 17.17
A certain right triangle has sides of length x, y, and z, where x < y < z. If the area of this triangular region is 1, which of the following indicates all of the possible values of y?
If abc = b3 , which of the following must be true?
I. ac = b2
II. b = 0
III ac = 1
Which of the following is NOT a root of the equation (x² + x - 20)² - 2(x² + x - 20) - 63 = 17
What is the sum of all possible solutions of the equation |x + 4|2 - 10|x + 4| = 24?
k is a positive integer and 225 and 216 are both divisors of k. If k=2a x 3b x 5c, where a, b and are positive integers, what is the least possible value of a+b+c?
A fair die is rolled once and a fair coin is flipped once. What is the probability that either the die will land on 3 or that the coin will land on heads?
If n = 4p, where p is a prime number greater than 2, how many different positive even divisors does n have, including n ?

Rectangle ABCD is comprised of 4 right triangles and rectangle FGHI. Triangles ADI and CBG are identical, and each has an area of 96. Triangles AFB and CHD are identical, and each has an area of 150. If the sides of each triangle have integer lengths, what is the area of rectangle FGHI?
A car traveled 462 miles per tankful of gasoline on the highway and 336 miles per tankful of gasoline in the city. If the car traveled 6 fewer miles per gallon in the city than on the highway, how many miles per gallon did the car travel in the city?
|
30 tests
|