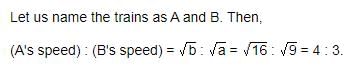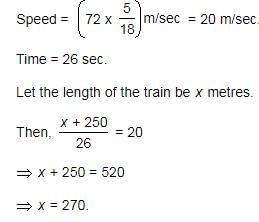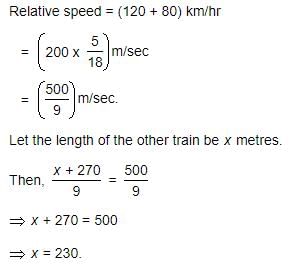Test: Problems On Trains- 1 (May 27) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - Test: Problems On Trains- 1 (May 27)
A train passes a platform in 36 seconds. The same train passes a man standing on the platform in 20 seconds. If the speed of the train is 54 km/hr, The length of the platform is:
A train moves past a post and a platform 264 m long in 8 seconds and 20 seconds respectively. What is the speed of the train?
Two trains having equal lengths, take 10 seconds and 15 seconds respectively to cross a post. If the length of each train is 120 meters, in what time (in seconds) will they cross each other when traveling in opposite direction?
Two trains, one from P to Q and the other from Q to P, start simultaneously. After they meet, the trains reach their destinations after 9 hours and 16 hours respectively. The ratio of their speeds is
A train having a length of 1/4 mile , is traveling at a speed of 75 mph. It enters a tunnel 3 ½ miles long. How long does it take the train to pass through the tunnel from the moment the front enters to the moment the rear emerges?
A train runs at the speed of 72 kmph and crosses a 250 m long platform in 26 seconds. What is the length of the train?
A train overtakes two persons who are walking in the same direction to that of the train at 2 kmph and 4 kmph and passes them completely in 9 and 10 seconds respectively. What is the length of the train?
A train is traveling at 48 kmph . It crosses another train having half of its length , traveling in opposite direction at 42 kmph, in 12 seconds. It also passes a railway platform in 45 seconds. What is the length of the platform?
A 270 metres long train running at the speed of 120 kmph crosses another train running in opposite direction at the speed of 80 kmph in 9 seconds. What is the length of the other train?
Two trains, each 100 m long are moving in opposite directions. They cross each other in 8 seconds. If one is moving twice as fast the other, the speed of the faster train is
|
152 docs|327 tests
|