Test: Projectile Motion - NEET MCQ
10 Questions MCQ Test Physics Class 11 - Test: Projectile Motion
Which one of the following is not an example of projectile?
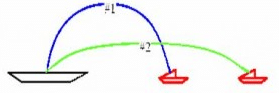
A battle ship simultaneously fires two shells at enemy ships. Both are fired with the same speed but with different directions as shown. If the shells follow the parabolic trajectories shown, which ship gets hit first?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If an object is dropped through the window of a fast running train. Then
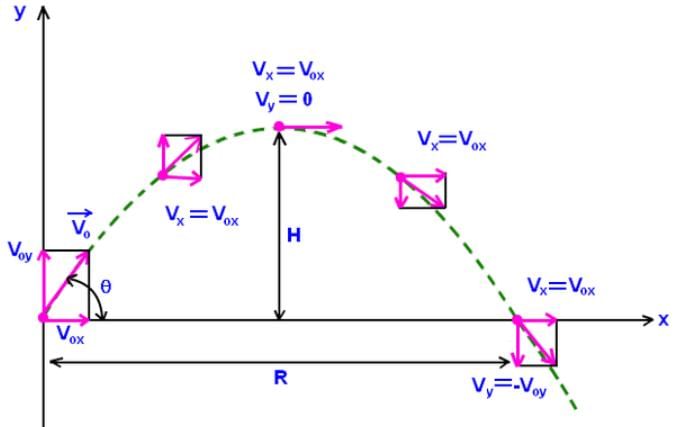
Which statement is true for a ball thrown at 20 degrees with the horizontal, when it is at the highest point in its trajectory?
How many directions are possible for the same horizontal range?
A body is thrown with a velocity of 10m/s at an angle of 60 degrees with the horizontal. Its velocity at the highest point is:
The quantity which remains unchanged during the flight of an oblique projectile is
At what angle should a projectile with initial velocity ‘v’ be thrown, so that it achieves its maximum range?
When a projectile is thrown up at an angle θ to the ground, the time taken by it to rise and to fall are related as
|
97 videos|378 docs|103 tests
|