Test: Properties of Tangents
15 Questions MCQ Test Online MCQ Tests for Class 10 | Test: Properties of Tangents
PT is a tangent from an external point P and PAB is a secant. If PT = 6cm and PA = 3cm, then the length of PB is __
We know that:
PT2 = PA X PB
therfore PB = PT2/PA = 36/3 = 12
A circle is inscribed in a ΔABC having AB = 10cm, BC = 12cm and CA = 8cm and touching these sides at D, E, F respectively. The lengths of AD, BE and CF will be
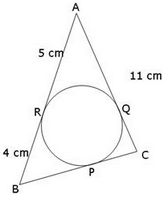
In the given figure, AR = 5cm, BR = 4cm and AC = 11cm. What is the length of BC?
Since the sides of the triangles are tangent to the circle. BR = BP,AR = AQ and CP = CQ
So, BP = 4cm and AQ = 5
CQ = 11-5 = 6 = CP
BC = BP + CP = 4 + 6 = 10 cm
In given figure, the length of BC is
Segment joining the points of contact of two parallel tangents
In a circle with centre O, AB and CD are two diameters perpendicular to each other. The length of chord AC is
If in the given figure radius of smaller and larger circles be 4 and 5 cm. Find the length of chord AB.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is :
The maximum number of common tangents that can be drawn to two circles intersecting at two distinct point is
In a circle of radius 7cm, tangent PT is drawn from point P such that PT = 24cm. If O is the centre of the circle, then the length of OP is:
In the figure, PQ is a tangent at a point R of the circle with centre O. If ∠TRQ = 30°.The measure of ∠PRS is
In the given figure, length of BC is:
ABC is a right triangle right angled at B such that BC = 6 cm and AB = 8 cm. The radius of its incircle is
By pythagoras theorem ,
H2 = P2 + B2
=36 + 64=100
H=10
We have a square BPOQ so all sides are equal.
Since tangents from a point are equal in length
Let AP = AR = x
BP=BQ=y
RC = QC = z
x + y = 8
x = 8 - y
x + z = 10 ⇒ 8 - y + z = 10 ⇒ z = 2 + y
y + z = 6 ⇒ y + 2 + y = 6 ⇒ y = 2
x = 6, z= 4
Since BP = OQ = y = 2
Quadrilateral ABCD circumscribes a circle as shown in figure. The side of the quadrilateral which is equal to AP + BR is:
If the angle between two radii of a circle is 100°, then angle between the tangents at the ends of those radii is:
 |
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
Recommended Content
 |
|
 |
 |
|
 |
|
 |
|
Recommended Tests
 |
|
|
|
|
|
|
|
|
|
Download free EduRev App
Similar Content
 |
|
|
|
 |
|
Related tests
|
|
|
|
|
|
|
|
|
|
|
© EduRev
|
Follow Us
|