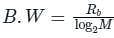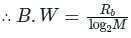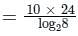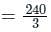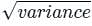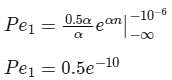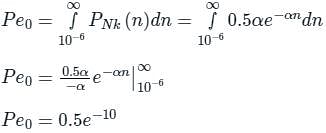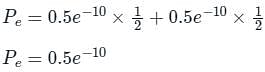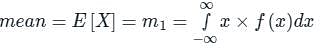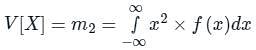Test: Pulse Amplitude Modulation (PAM) - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test GATE ECE (Electronics) Mock Test Series 2025 - Test: Pulse Amplitude Modulation (PAM)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
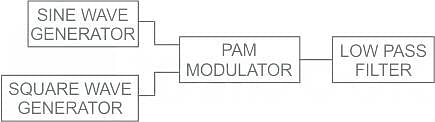
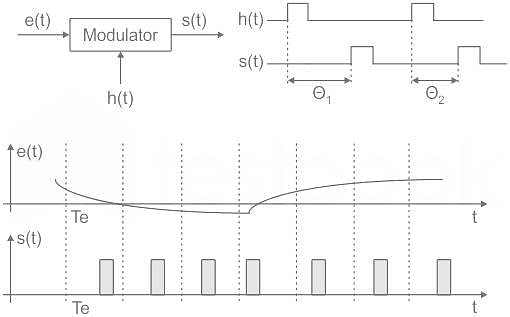
Which filter is used to detect the PAM signal?
A speech signal is sampled a rate of 20% above the Nyquist rate. The signal has a bandwidth of 10 kHz. The sample is quantized into 1024 levels and then transmitted through 8-level PAM over an AWGN baseband channel. The bandwidth required for transmission is ______
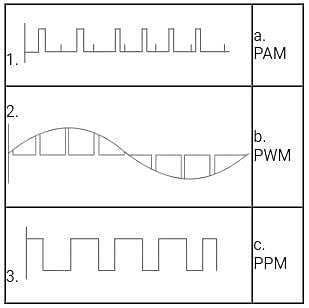
Which of the following Pulse time Modulation does not exist in practice?
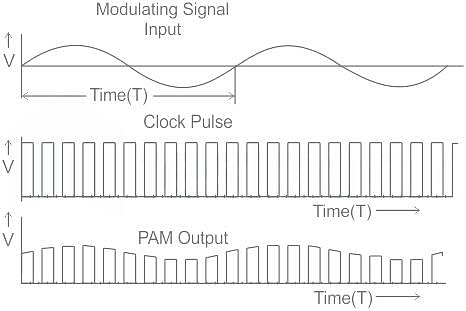
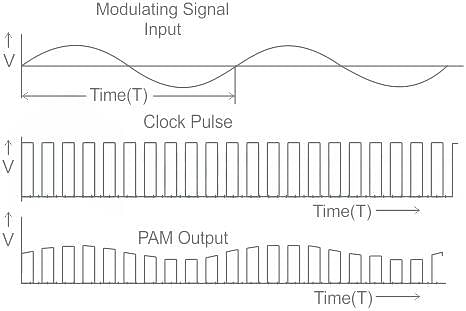
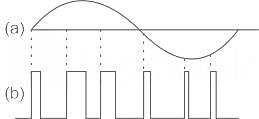
Study the given input signal and match the columns.
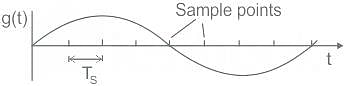
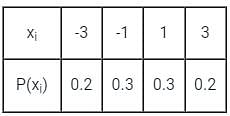
A PAM source generates four symbols 3 V, 1 V, -1 V and -3 V with probability of p(3) = p(-3) = 0.2 and p(1) = p(-1) = 0.3 respectively. The variance for the source will be
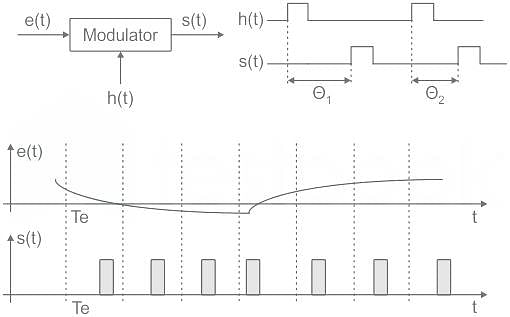
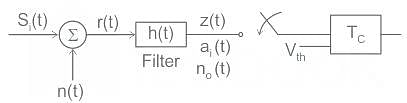
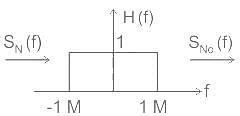
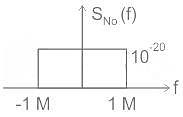
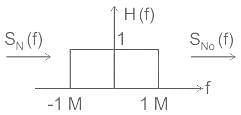
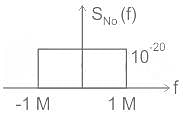
Consider a baseband binary PAM receiver shown below. The additive channel noise n(t) is white with power spectral density SN(f) = N0/2 = 10-20 W/Hz. The low-pass filter is ideal with unity gain and cutoff frequency 1 MHz. Let Yt, represent the random variable y(t1)
Yt = Ns if transmitted bit bk = 0
YK = a + Nk if transmitted bit bk = 1
where Nk represents the noise sample value. The noise sample has a probability density function, PN (n) = 0.5αe (This has mean zero and variance 2/α2), Assume transmitted bits lo be equiprobable and threshold z is set to a/2 = 10-6 V
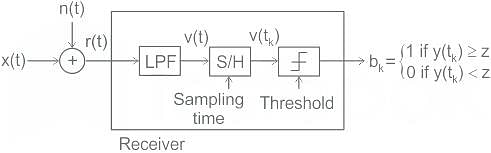
‘The probability of bit error is
Consider a baseband binary PAM receiver shown below. The additive channel noise n(t) is white with power spectral density SN(f) = N0/2 = 10-20 W/Hz. The low-pass filter is ideal with unity gain and cutoff frequency 1 MHz. Let Yt, represent the random variable y(t1)
Yt = Ns if transmitted bit bk = 0
YK = a + Nk if transmitted bit bk = 1
where Nk represents the noise sample value. The noise sample has a probability density function, PN (n) = 0.5αe (This has mean zero and variance 2/α2), Assume transmitted bits lo be equiprobable and threshold z is set to a/2 = 10-6 V
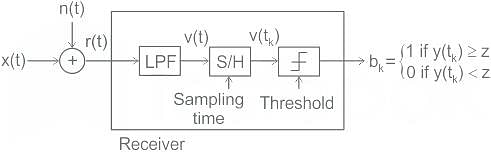
Q. The value of the parameter α (in V-1) is
Which of the following is NOT an advantage of Pulse Duration Modulation (PDM) recording?
|
25 docs|263 tests
|
|
25 docs|263 tests
|