Test: Quadratic Equations- 2 - Railways MCQ
20 Questions MCQ Test - Test: Quadratic Equations- 2
A number x is multiplied with itself and then added to the product of 4 and x. If the result of these two operations is -4, what is the value of x?
If x and y are non-zero numbers, what is the value of x/y?
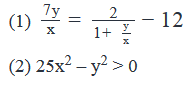
If one of the roots of the quadratic equation x2 + bx + 98 = 0 is the average (arithmetic mean) of the roots of the equation x2 + 28x – 588 = 0, what is the other root of the equation x2 + bx + 98 = 0?
If
where the given expression extends till infinity, which of the following statements must be true ?
I. Two values are possible for z
II. 4 - z2 = 2
III. z8 = 16
r and s are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0 & s >0, such that r is 50 percent greater than s. If the product of the roots of the equation is 150, what is the sum of the roots of the equation?
For a quadratic equation, both the product of the roots and the sum of the roots are prime numbers less than 10. If both the roots are integers, what is the difference between the roots?
A quadratic equation ax2 + bx + c = 0 has two integral roots x1 and x2. If the square of the sum of the roots is 6 greater than the sum of the squares of the roots, which of the following could be the value of the ordered set (a, b, c)?
I. (-1, 4, -3)
II. (1, 4, 3)
III. (3, -10√3, 9)
x and y are integers such that xy < 0. If x2 – y2 = 0, what is the value of y?
(1) 2x2 – 21x – 36 = 0
(2) y2 = (-1)n (12y), where n is a positive integer not divisible by 2.
If p and q are the roots of the quadratic equation ax2 + bx + c = 0 where a ≠ 0, what are the roots of the equation ayx2 + byx + cy = 0 where 0 < y ≤ 1?
Given the three quadratic equations above, which pair of equations has at least one common root?
if 2x2 = 24 -x4 and which of the following can be the value of x?
If x is a negative number, what is the value of x?
(1) 16x2 – 16x – 5 = 0
(2) ||4x+3| - 5| = 3
Edward invested five-ninths of his money at an annual rate of 2r% compounded semi-annually, and the remaining money at an annual rate of r% compounded annually. If after one year, Edward’s money had grown by one-thirds, the value of r is equal to which of the following?
If x is equal to , where the given expressions extend to an infinite number of roots, then what is the value of x?
If p and q are the roots of the quadratic equation ax2 + bx + c = 0, where a*b*c ≠ 0, is the product of p and q greater than 0?
(1) |p + q| = |p| + |q|
(2) ac > 0
The area of a rectangle is 28 square centimeter. What is the perimeter of the rectangle?
(1) If the length of the rectangle is increased by 10 centimeter and the breadth is decreased by 5 centimeter, the perimeter of the rectangle is eight times the original length of the rectangle.
(2) If the length of the rectangle is increased by 350% and the breadth is increased to 350% of the original breadth, the perimeter of the rectangle is 63 centimeters more than the original perimeter of the rectangle.
What are the roots of the quadratic equation x2 + bx + c = 0 if the roots are distinct and at equal distance from 5 on the number line?
(1) The product of the roots of the equation x2 + bx + c = 0 is 21
(2) x – 7 is a factor of the expression 7x2 + 7bx + 7c
If x2+4x+p=13 , where p is a constant, what is the product of the roots of this quadratic equation?
(1) -2 is one of the roots of the quadratic equation
(2) x2+4x+p=13 has equal roots
x2 + bx + 72 = 0 has two distinct integer roots; how many values are possible for 'b'?














