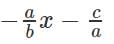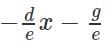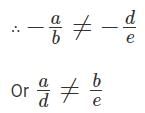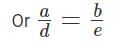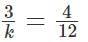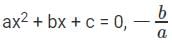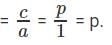Test: Quadratic Equations- 3 - GMAT MCQ
15 Questions MCQ Test - Test: Quadratic Equations- 3
A poultry farm has only chickens and pigs. When the manager of the poultry counted the heads of the stock in the farm, the number totaled up to 200. However, when the number of legs was counted, the number totaled up to 540. How many more chickens were there in the farm? Note: In the farm, each pig had 4 legs and each chicken had 2 legs.
Three years back, a father was 24 years older than his son. At present the father is 5 times as old as the son. How old will the son be three years from now?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
For what values of 'k' will the pair of equations 3x + 4y = 12 and kx + 12y = 30 NOT have a unique solution?
The basic one-way air fare for a child aged between 3 and 10 years costs half the regular fare for an adult plus a reservation charge that is the same on the child's ticket as on the adult's ticket. One reserved ticket for an adult costs $216 and the cost of a reserved ticket for an adult and a child (aged between 3 and 10) costs $327. What is the basic fare for the journey for an adult?
Numbers: All numbers used are real numbers.
Figures: A figure accompanying a data sufficiency question will conform to the information given in the question but will not necessarily conform to the additional information given in statements (1) and (2)
Lines shown as straight can be assumed to be straight and lines that appear jagged can also be assumed to be straight
You may assume that the positions of points, angles, regions, etc. exist in the order shown and that angle measures are greater than zero.
All figures lie in a plane unless otherwise indicated.
Q.
Is y = 3?
- (y - 3)(x - 4) = 0
- (x - 4) = 0
A children's gift store sells gift certificates in denominations of $3 and $5. The store sold 'm' $3 certificates and 'n' $5 certificates worth $93 on a Saturday afternoon. If 'm' and 'n' are natural numbers, how many different values can 'm' take?
What is the highest integral value of 'k' for which the quadratic equation x2 - 6x + k = 0 will have two real and distinct roots?
If one of the roots of the quadratic equation x2 + mx + 24 = 0 is 1.5, then what is the value of m?
For what value of 'm' will the quadratic equation x2 - mx + 4 = 0 have real and equal roots?
y = x2 + bx + 256 cuts the x axis at (h, 0) and (k, 0). If h and k are integers, what is the least value of b?
x2 + bx + 72 = 0 has two distinct integer roots; how many values are possible for 'b'?
If x > 0, how many integer values of (x, y) will satisfy the equation 5x + 4|y| = 55?
If p > 0, and x2 - 11x + p = 0 has integer roots, how many integer values can 'p' take?
How many real solutions exist for the equation x2 – 11|x| - 60 = 0?
If the curve described by the equation y = x2 + bx + c cuts the x-axis at -4 and y axis at 4, at which other point does it cut the x-axis?