Test: Quantitative Reasoning (Level 500) - GMAT MCQ
21 Questions MCQ Test Practice Questions for GMAT - Test: Quantitative Reasoning (Level 500)
Six machines, each working at the same constant rate, together can complete a certain job in 12 days. How many additional machines, each working at the same constant rate, will be needed to complete the Job in 8 days?
Jan lives x floors above the ground floor of a highrise building. It takes her 30 seconds per floor to walk down the steps and 2 seconds per floor to ride the elevator. If it takes Jan the same amount of time to walk down the steps to the ground floor as to wait for the elevator for 7 minutes and ride down, then x equals
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Three positive numbers x, y, and z have the following relationships y = x + 2 and z = y + 2. When the median of x, y, and z is subtracted from the product of the smallest number and the median, the result is 0. What is the value of the largest number?
When positive integer m is divided by positive integer n, the remainder is 12. If m/n = 24.2, what is the value of n ?
In an election between two candidates, one got 52% of total valid votes. 25% of the total votes were invalid. The total number of votes were 8400. How many valid votes did the other person get?
What is the least possible product of 5 different integers, each of which is between –5 and 5, inclusive?
A chemistry student has one solution that’s 25 percent saline and another that’s 15 percent saline. Approximately how many liters of the 25 percent solution must be added to the 15 percent solution to make 10 liters of a solution that’s 20 percent saline?
Which of the following inequalities represents the entire solution set for x if |x| > x?
The edges of a cube are made out of wire. If the surface area of that cube is 24, what is the total length of the wire?
Of the 400 cadets in a graduating class, 30 percent were women and, of these, 1/5 became instructors. If the number of men who became instructors was twice the number of women who became instructors, how many of the men became instructors?
The boy ans girls in a college are in the ratio 3: 2. If 20% of the boys and 25% of the girls are adults , the percentage of the students who are not adults ?
Two cars started from the same point and traveled on a straight course in opposite directions for exactly 3 hours, at which time they were 300 miles apart. If one car traveled, on average, 10 miles per hour faster than the other car, what was the average speed of the slower car for the 3-hour trip?
What is the sum of the even integers between 200 and 400, inclusive?
When Leo imported a certain item, he paid a 7 percent import tax on the portion of the total value of the item in excess of $1,000. If the amount of the import tax that Leo paid was $87.50, what was the total value of the item?
Of the 500 business people surveyed, 78 percent said that they use their laptop computers at home, 65 percent said that they use them in hotels, and 52 percent said that they use them both at home and in hotels. How many of the business people surveyed said that they do not use their laptop computers either at home or in hotels?
When traveling at a constant speed of 32 miles per hour, a certain motorboat consumes 24 gallons of fuel per hour. What is the fuel consumption of this boat at this speed measured in miles traveled per gallon of fuel?
If x is an integer, what is the value of x such that |-5x + 7| is minimized?
If it would take one machine 10 minutes to fill a large production order and another machine 12 minutes to fill the same order, how many minutes would it take both machines working together, at their respective rates, to fill the order?
There are 10 players in a chess group, and each player plays each of the others once. Given that each game is played by two players, how many total games will be played?
The lunch menu at a certain restaurant contains 4 different entrees and 5 different side dishes. If a meal consists of 1 entree and 2 different side dishes, how many different meal combinations could be chosen from this menu?
|
18 docs|139 tests
|


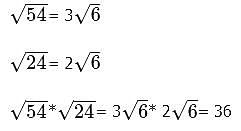
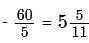 minutes
minutes















