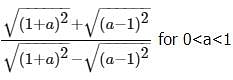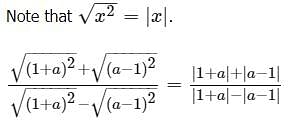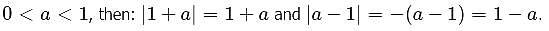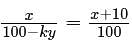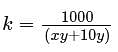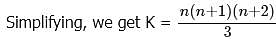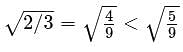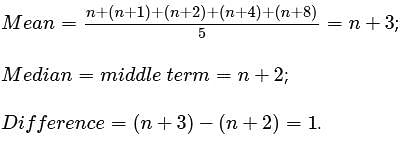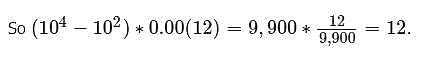Test: Quantitative Reasoning (Level 700) - 2 - GMAT MCQ
21 Questions MCQ Test Practice Questions for GMAT - Test: Quantitative Reasoning (Level 700) - 2
A beaker contains 100 milligrams of a solution of salt and water that is x% salt by weight such that x < 90. If the water evaporates at a rate of y milligrams per hour, how many hours will it take for the concentration of salt to reach (x+10)%, in terms of x and y?

In the multiplication above, each letter stands for a different non-zero digit, with A x B < 10. What is the two-digit number AB?

Find the numbers of ways in which 4 boys and 4 girls can be seated in a row of 8 seats if they sit alternately and if there is a boy named John and a girl named Susan amongst this group who cannot be put in adjacent seats ?
The ‘moving walkway’ is a 300-foot long walkway consisting of a conveyor belt that moves continuously at 3 feet per second. When Bill steps on the walkway, a group of people that are also on the walkway stands 120 feet in front of him. He walks toward the group at a rate of 3 feet per second. Once Bill reaches the group of people, he stops walking and stands with them until the walkway ends. What is Bill’s average rate of movement for his trip along the moving walkway?
Five integers in a set are written ascending order. The median of this set is 17, and the average of the smallest and largest integers is 16. When the smallest and largest numbers are removed from the set, the average of the new smallest and largest integers is 15. What can be the minimum value of the largest of the original five integers?
The sum of the digits of a positive integer N is 23. The remainder when N is divided by 11 is 7. What is the remainder when N is divided by 33?
100 people are attending a newspaper conference. 45 of them are writers and more than 38 are editors. Of the people at the conference, x are both writers and editors and 2x are neither. What is the largest possible number of people who are both writers and editors?
Diana is going on a school trip along with her two brothers, Bruce and Clerk. The students are to be randomly assigned into 3 groups, with each group leaving at a different time. What is the probability that DIana leaves at the same time as AT LEAST on her bothers?
K = 1*2+2*3+________+21*22
What is the remainder when K is divided by 23?
Rank the following quantities in order, from smallest to biggest.
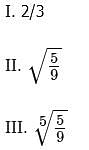
A manufacturer produces a certain men's athletic shoe in integer sizes from 8 to 17. For this particular shoe, each unit increase in size corresponds to a 1/4-inch increase in the length of the shoe. If the largest size of this shoe is 20% longer than the smallest size, how long, in inches, is the shoe in size 15?
A certain thermometer measured the temperature in City X in degreed Fahrenheit every day for one month, and found that the range of temperatures was 21 degrees. If, subsequently, it was discovered that the thermometer always overstated the temperature by 15%, what would the approximate range of measurements have been, in degrees, if the temperatures had been measured accurately?
Two candles of the same height are lighted at the same time. The first candle is consumed in 4 hours and the second one in 3 hours. Assume that each candle burns at the same rate. In how many hours will the first candle measure twice the height of the second candle?
40 men and 20 women together can complete a work in 12 days and ratio of efficiency of a man to a woman is 2:3, find how many men are required to complete half of the work in 7 days?
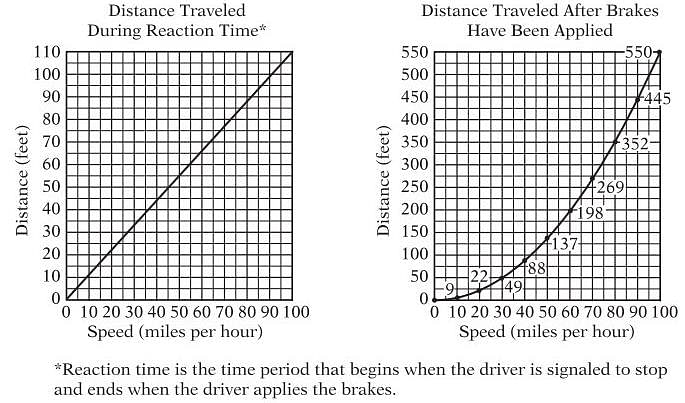
Note: Total stopping distance is the sum of the distance traveled during reaction time and the distance traveled after brakes have been applied.
Of the following, which is the greatest speed, in miles per hour, at which the car can travel and stop with a total stopping distance of less than 200 feet?
C individuals pledged to pay equal contributions so that a charity’s goal of $x could be reached. If d of the contributors failed to pay their share, which of the following represents the additional number of dollars that each of the remaining individuals would have to pay in order to allow the charity to reach its goal?

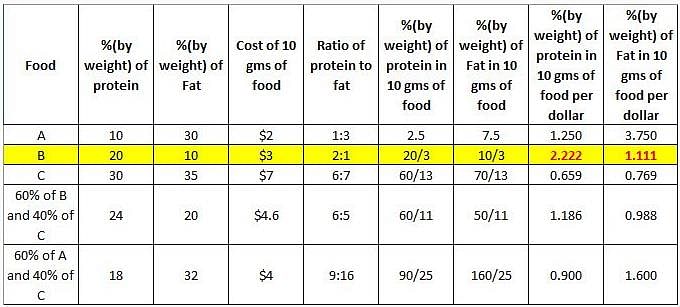
Which one of the following diets or the combination of diets supplies more protein for every dollar?
For the positive numbers, n, n + 1, n + 2, n + 4, and n + 8, the mean is how much greater than the median?
A bar over a sequence of digits in a decimal indicates that the sequence repeats indefinitely. What is the value of 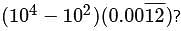
For any integer P greater than 1, P! denotes the product of all integers from 1 to P, inclusive. A number is chosen at random from the list of factors of 8!. What is the probability that the chosen number is a multiple of 28?
|
18 docs|139 tests
|