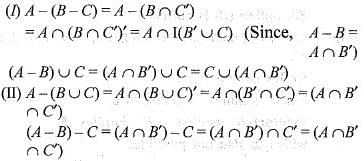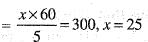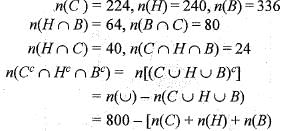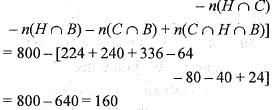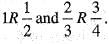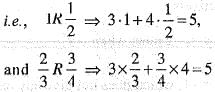Test: Real Analysis- 8 - Mathematics MCQ
20 Questions MCQ Test Topic-wise Tests & Solved Examples for Mathematics - Test: Real Analysis- 8
Let R and S be two non-void relations on a set A.
Q. Which of the following statements is false?
Q. Which of the following statements is false?
Consider the following statements
For non-empty sets A, B and C
1. A - (B - C) = (A - B) ∪ C
2. A - (B - C) = (A - B) - C
Q. Which of the statements given above is/are correct?
For non-empty sets A, B and C
1. A - (B - C) = (A - B) ∪ C
2. A - (B - C) = (A - B) - C
Q. Which of the statements given above is/are correct?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Let N be the set of integers. A relation R on N is defined as R = {(x, y) | xy > 0, x, y ∈ N}. Then, which one of the following is correct?
Which one of the following function f : R → R is injective?
If A is the set of even natural number less than 8 and B is the set of prime number less than 7, then number of relations from A to B is
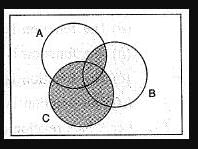
What does the shaded region in the Venn diagram given following represent?

Out of 32 persons, 30 invest in National savings Certificates and 17 invest in shares. What is the number of persons who invest in both?
Let R = {x | x ∈ N ,x is multiple of 3 and x ≤ 100} and S = {x | x ∈ N, x is a multiple of 5 and x ≤ 100} What is the number of elements in (R x S) ∩ (S x R) ?
Let X be the set of all graduates in India. Elements x and y in X are said to be related, if they are graduates of the same university. Which one of the following statements is correct?
In a college of 300 students, every student reads 5 newspaper and every newspaper is read by 60 students. The number of newspaper is
Out of 800 boys in a school, 224 played cricket, 240 played hockey and 336 played basketball. Of the total, 64 played both basketball and hockey; 80 played cricket and basketball and 40 played cricket and hockey; 24 played all the three games. The number of boys who did not play any game is
Let A = {-1, 2, 5, 8}, B = {0, 1, 3, 6, 7} and R be the relation ‘is one less than’ from A to B, then how many elements will R contain?
Consider the function f:R → {0, 1} such that

Q. Which one of the following is correct?
Let R be a relation over the set N x N and it is defined by (a, b)R (c, d) ⇒ a + d = b + c. Then R is
Let N denote the set of natural numbers and A = {n2 : n ∈ N} and B = {n3/2 : n ∈ N}. Which one of the following is correct?
If A and. B are two disjoint sets, then which one of the following is correct?
Let M be the set of men and R is a relation ‘is son of’ defined on M. Then, R is
Let f : R --> R be a function defined a s / ( x ) = x | x |; for each x ∈ R, R being the set of real numbers. Which one of the following is correct?
Consider the following with regard to a relation R on a set of real number defined by xRy if and only if 3x + 4y = 5.
1. 0R1
2. 1R1/2
3. 2/3R3/4
Q. Which of the above are correct?
|
27 docs|150 tests
|