Test: Rectangles And Squares- 2 - GRE MCQ
20 Questions MCQ Test - Test: Rectangles And Squares- 2
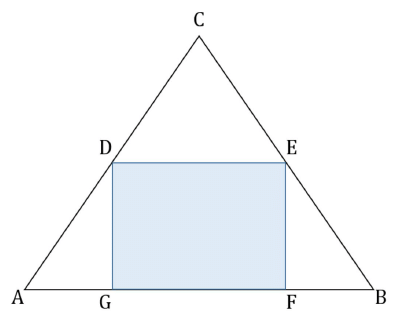
Rectangle DEFG is inscribed in equilateral triangle as shown above. What is the area of triangle ABC?
(1) The area of rectangle DEFG is 8√3 square units
(2) The area of triangle AGD is 2√3 square units
(1) The area of rectangle DEFG is 8√3 square units
(2) The area of triangle AGD is 2√3 square units
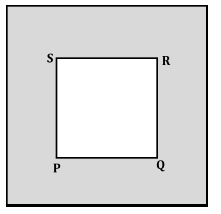
A frame of uniform width is placed around a square photograph PQRS. If PQ = 10 inches and the area of the frame is 125 square
inches, what is the width of the frame, in inches?
inches, what is the width of the frame, in inches?
The rectangle ABCD has its side lengths equal to x and y respectively, where x and y are prime numbers greater than 2. Which of the following cannot be equal to the sum of all the sides of the rectangle ABCD?
I. 64
II. 82
III. 146
I. 64
II. 82
III. 146
A wire was initially used to fence a right-triangular plot of land along its perimeter. The lengths, in metres, of the perpendicular sides of the plot were both integers and in the ratio 3:4. The wire was later removed from the triangular plot and used to fence a square plot along its perimeter. When the square plot had been completely fenced, 4 metres of wire still remained. Which of the following could represent the greatest distance between two points in the square plot?
A student initially draws a rectangle ABCF. Later, he draws an adjacent trapezium FCDE in which side ED is parallel to side FC and drops perpendiculars EG and DH on FC. The dimensions of each side of the polygon ABCDEF, in centimeters, are shown on the figure above. What is the value of x?
(1) The area of the polygon ABCHDEG is 332 square centimeters
(2) If sides AE and BD are joined, the area of the quadrilateral ABDE will be 266 square centimeters
In the figure above, a regular hexagon EFGHIJ is inscribed in the rectangle ABCD. If the ratio of the magnitudes of the area and the perimeter of the hexagon is √3/2 , what is the ratio of the magnitudes of the area and the perimeter of the rectangle ABCD?
In the figure given above, ABCD is a rectangle that is divided into five triangular regions. If triangles I, II and III have equal area and triangles IV and V have equal area, what is the area of rectangle ABCD?
(1) The area of triangle I is 30
(2) The area of triangle V is 15
Two identical square paintings are pasted on a rectangular wooden display board such that the edges of each painting are parallel to the corresponding edges of the display board and the two paintings are symmetrical about an imaginary line passing through the middle of the display board. The margins between the paintings and between the paintings and the board are as shown in the figure above. If the area of the display board is 66 square units, what is the area of each square painting?
A flowerbed of uniform width is developed around a rectangular patch of grass such that the outer length of the flowerbed is two-thirds more than the length of the rectangular patch and the outer breadth of the flowerbed is 100 percent greater than the breadth of the rectangular patch. If the area of the flowerbed is 8 square units more than twice the area of the rectangular patch, what is the area of the rectangular patch of grass?
In the xy-coordinate plane, polygon APBCDA is formed by placing rectangle ABCD and triangle APB as shown above. If sides AB and AD are parallel to the x- and the y- axes respectively, what is the area of polygon APBCDA?
(1) The coordinates of points A and C are (6, 8) and (12, 12) respectively
(2) The coordinates of point P are (8, 10)
The length of a rectangle is 2 units greater than its breadth. If a diagonal of the rectangle measures 10 units, what is the perimeter of the rectangle?
In the figure above, ABCD is a quadrilateral in which sides AB and CD are parallel. What is the area of the quadrilateral?
(1) The distance between sides AB and CD is 4 units
(2) The length of side AD is √17 units
If parallelogram ABCD has a perimeter of 12 units and ∠ADC = 120 , what is the area of the parallelogram?
(1) BD = 2√3 units
(2) The distance between sides AB and CD is √3 units
The figure above shows the walking path in a park, which is to be covered with tiles. Paths A and path B are semi-circular in shape with the radius of the inner boundary of the path being equal to 8 feet and 4 feet respectively. If the cost of laying the tiles is $5 per square feet and the path has a uniform width of 2 feet across the park, which of the following is the closest to the amount it will cost, in dollars, to cover the complete walking path with tiles?
Is one of the angles of the quadrilateral ABCD equal to 90 degrees?
(1) ABCD is a parallelogram
(2) One of the interior angles of ABCD is equal to 60 degrees
What is the area of rectangle ABCD?
(1) The length of side AB is 2 units more than the length of side BC.
(2) The length of the diagonal AC is 10 units.
In the figure given above, a rectangular photograph is placed in a black frame that has a uniform width of x centimeters between the photograph and the outer boundary of the frame. If the difference between the perimeter of the photograph and of the outer boundary of the frame is 32 centimeters, what is the width in centimeters of the black frame?
In the given figure ABCD is a rectangle and EF || AD. AEG and FEB are two triangles inscribed in the rectangle ABCD such that the area of triangle AEG is half of the area of triangle FEB. What is the area of rectangle ABCD?
(1) EBCF is a square of side length 5 centimeters.
(2) A line passing through point G and parallel to AB divides the rectangle ABCD into 2 equal halves
In the figure given above, the diagonal AC and side DC of square ABCD are extended to form sides of the isosceles triangle CEF where CE = EF. If the length of side CF is 2√2 and the ratio of areas of the triangle CEF to the square ABCD is 1:8, what is the length of the side of square ABCD?
Square ABCD and Trapezium PQRS lie between the parallel lines l and m as shown in the figure above. If the area of the square ABCD and trapezium PQRS is equal to 64 square centimeters each, what is the length in centimeters of PQ?



















