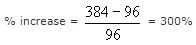Test: Rectangular Solids- 1 - GMAT MCQ
15 Questions MCQ Test - Test: Rectangular Solids- 1
A rectangular container X has a total capacity of 5 cubic feet. If each dimension of X is multiplied by a positive number D, then a new rectangular container Y is formed. If Y has a total capacity of 135 cubic feet. What is the value of D?
Area of 3 adjacent faces of a rectangular solid are x2, 4x and 16x respectively where ‘x’ is a positive integer. What is the volume of this solid (in terms of x)?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
What is the largest possible diagonal (in cms) of a fish tank (in the form of a rectangular solid), if it is 20cms long, 10 cms wide and 20 cms high?
1/3rd of a large can X in the shape of a right circular cylinder is filled with cola. If the volume of cola in the can is 12 cubic inches and the radius of the can is 6 inches, then what is the height of the can X?
A large can in the shape of a right circular cylinder has a total capacity of 16π cubic inches. When completely filled, this cylinder can fill to capacity exactly 4 equal smaller cans (right circular cylinder) of height 1 inch each. What is the radius (in inches) of a smaller can?
A certain right circular cylinder is filled halfway with g gallons of water. When placed on its side, the maximum depth of the water is c centimeters. In terms of c and g , what is the height of the cylinder?
In the rectangular solid above, BCDE is a square and the dotted line connecting A to E is twice the length of edge EB. If edge AB is √3, what is the volume of the solid?
What is the volume of a certain cube?
(1) Each face of the cube has an area of 5
(2) The longest possible straight-line distance between any two points of the cube is √15
Two cylindrical buckets – A and B – contain only water. Three-fourths of bucket A’s volume is occupied by water while one-fourths of bucket B’s volume is occupied by water, When all the water in bucket A is poured into bucket B, bucket B gets exactly half-filled. If the radius of the base area of bucket A is twice the radius of base area of bucket B, and the height of bucket B is 2 metres, what is the height of the container A in metres?
Three identical cylinders are inscribed within a rectangular solid, shown above from the top. If the length of the rectangular solid is 4 feet and the height (not shown) is 2 feet, what is the volume of the rectangular solid?
If right circular cylinders A and B have the same radius : height ratio, what is the ratio of the curved surface area of cylinder A to the curved surface area of cylinder B?
(1) The ratio of the radius of cylinder A to the radius of cylinder B is 2:1
(2) The ratio of the volume of cylinder A to the volume of cylinder B is 8:1
If the length of each edge of a certain rectangular solid is an integer and exactly four of its faces have the same dimensions, then what is the volume of the rectangular solid?
(1) Two of the faces have areas of 32 square units and 16 square units.
(2) One of the edges is twice the length of another edge.
What is the greatest possible (straight-line) distance between any two points on a certain rectangular solid of length L, width W, and height H, where H < W < L ?
(1) The length, width, and height of the rectangular solid are the squares of prime integers.
(2) The roots of the equation x2 – 13x = -36 are the width and the height of the rectangular solid.
A 4 cm cube is cut into 1 cm cubes. What is the percentage increase in the surface area after cutting?
A regular hexagon is inscribed in a circle of radius r cm. What is the perimeter of the regular hexagon?