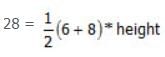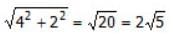Test: Rectangular Solids- 2 - GMAT MCQ
20 Questions MCQ Test - Test: Rectangular Solids- 2
A toy is in the form of a right circular cone mounted on a hemisphere. If the height of the cone is twice the radius of the cone and the total height of the toy is 15 centimeters, what is the volume of the hemisphere in cubic centimeters? (The volume of a sphere is 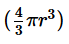 , where r is the radius)
, where r is the radius)
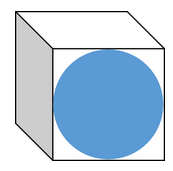
The figure above shows a cube one of whose faces has been painted with a blue circle that touches each edge of the face. If all the other faces of the cube are also to be painted in a similar manner, how much surface area of the cube will be left unpainted?
(1) The surface area of the cube is 1944 square units
(2) The area of the blue circle is 81π square units
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
A rectangular solid brick of iron is melted and shaped into a cube. If the areas of different sides of the brick were 24, 36 and 54 square units respectively, what is the surface area of the cube in square units?
By looking at a rectangular box, a carpenter estimates that the length of the box is between 2 to 2.1 meters, inclusive, the breadth is between 1 to 1.1 meters, inclusive and the height is between 2 to 2.1 centimeters, inclusive. If the actual length, breadth and height of the box do indeed fall within the respective ranges estimated by the carpenter, which of the following is the closest to the maximum possible magnitude of the percentage error that the carpenter can make in calculating the volume of the rectangular box?
A right circular cylinder having the radius of its base as 2 centimeters is filled with water upto a height of 2 centimeters. This water is then poured into an empty rectangular container the dimensions of whose base are 2π by 3 centimeters. If the volume of water in the rectangular container is increased by 50 percent by adding extra water, what is the final height, in centimeters, of the water level in centimeters in the rectangular container?
What is the longest distance between two points in a rectangular solid if the area of its faces is 50, 75 and150 square units respectively?
Water is taken out of a cylindrical bucket by filling a cylindrical mug to the brim. How many mugs of water does the bucket contain?
- The height of the bucket is three times the height of the mug and the radius of the bucket is twice the diameter of the mug
- The bucket is filled to 70 percent of its capacity
A cube of side length x centimeters is placed on a floor. A cube of side length x/2 centimeters is placed at the center of the top of the cube of side length x centimeters. What fraction of the total surface area of the cubes is visible?
If a cube of side length 24 units is cut into 512 smaller cubes of equal dimensions, then what is the ratio of the combined surface area of the smaller cubes and the surface area of the original cube?
A hall is in the form of a rectangular solid with its each side length equal to 12 feet. If the floor and one wall of the hall are to be covered with colored tiles measuring 2 feet by 2 feet, how many such tiles are required?
The volume of a sphere with radius r is and the surface area is 4πr2. If a solid spherical ball of iron with radius r centimetres is cut into two equal hemispheres, what is the ratio, in terms of r, of the volume and the surface area of each hemisphere?
In the rectangular solid above, if each dimension of the rectangular solid is an integer greater than 1 and the area of two sides of the solid is 14 and 18 respectively, what is the volume of the solid?
The space diagonal of cube A is more than 2√6 units longer than the space diagonal of cube B and the surface area of cube A is 192 square units greater than the surface area of cube B. If the lengths of both cubes are integers, by how many cubic units is the volume of cube A greater than the volume of cube B?
A right circular cylinder of height 1 meter and radius 9√2 centimeters is to be used to store cubes of side length 3 cm each. If in each layer of cubes stored in the cylinder, the cubes are arranged such that the top view of the layer is a square, what is the maximum number of cubes that can be stored in the cylinder? (1 meter = 100 centimeters)
A right circular cylinder is cut parallel to its base into two halves. By what percentage is the combined total surface area of the smaller cylinders greater than the total surface area of the original cylinder?
(1) The sum of the radius and the height of the original cylinder is 3 times the radius of the original cylinder.
(2) If the original cylinder is melted and a part of the molten material is used to form into a sphere with the same radius as the original cylinder, the volume of the sphere thus formed will be 33 percent less than the volume of the original cylinder. (The volume of a sphere is , where r is the radius)
In a rectangular box of dimensions 20 centimetres by 20 centimetres by 100 centimetres, identical spherical balls are arranged in layers such that each layer has exactly 4 balls. The top view of this arrangement is shown in the figure above. What is the approximate percentage of space left empty inside the box, if the box contains the maximum possible number of layers of such spherical balls? (The volume of a sphere is , where r is the radius of the sphere)
In the rectangular solid above, if each dimension of the solid is an integer, what is the volume of the solid?
(1) The area of two sides of the rectangular solid is 4 and 20 respectively
(2) The area of two sides of the rectangular solid is 4 and 5 respectively.
A paint can is in the shape of a right circular cylinder. A rectangular paper label of area 12 square units is pasted on the can as shown in the figure.If the label can be wrapped around the can only once with no extra paper hanging out, what is the curved surface area of the paint can?
(1) The center of the paper label is at a distance of 5 units each from the top and the bottom of the can
(2) The height of the can is five times the height of the paper label.
If x units are added to the length of the radius of a circle, what is the number of units by which the circumference of the circle is increased?
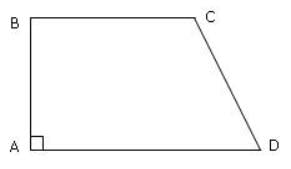
ABCD has area equal to 28. BC is parallel to AD. BA is perpendicular to AD. If BC is 6 and AD is 8, then what is CD?