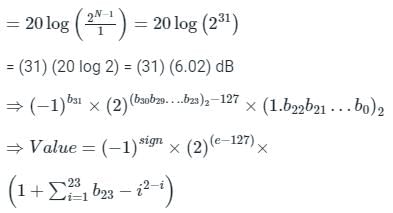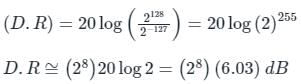Test: Representation of Signed Numbers - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Representation of Signed Numbers
Which of the following is the smallest 4-bit negative number stored in its 2's complement representation?
The I's complement of the binary number (101100)2 is:
Perform the subtraction and represent your answer in 2’s complement form (10010)2 - (10111)2
The difference in the dynamic range of 32-bit binary number(B) and floating-point number(F) is?
Standard Format for B and F as given below :
B=
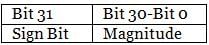
F=

No of bits required to represent -6410 in 2’s complement form:
The number of 1’s in the 8-bit unsigned representation of 127 in its 2’s complement form is m and that in 1’s complement form is n. What is the value of m : n?
A register contains a 2’s complement no 10100. Find the value of a register if it is divided by 2
X = 01110 and Y = 11001 are two 5-bit binary numbers represented in two’s complement format. The sum of X and Y represented in two’s complement format using 6 bits is
X = 00110 and Y = 10011 are two binary numbers represented in 2's complement format. The sum of X and Y represented in 2's complement format using 5 bits is _____