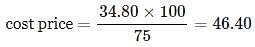Test: Sale And Purchase- 1 - GRE MCQ
15 Questions MCQ Test Quantitative Reasoning for GRE - Test: Sale And Purchase- 1
Product Y was sold after applying successive discounts of 20% and 30% on the list price (marked price). What is the list price of product Y if it was sold at $112?
A bicycle is sold after applying successive discounts of 10% and 20% on the list price at Shop A. The same is sold at a flat discount of 30% on the list price at Shop B. If the list price of bicycle is $200 for both Shop A and Shop B, what is the positive difference (if any) between the final prices of bicycles sold at Shop A and Shop B?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The marked price of an LCD television is 100% higher than the cost price. If it is sold at a price of $810 after applying two successive discounts of 10% each on the marked price, what is the cost price (in dollars) of LCD television?
The marked price of a garment is 100% higher than the cost price. If it is sold at a price of $112 after applying successive discounts of 20% and 30% on the marked price, what is the profit (in dollars) obtained by selling the garment?
The marked price of Brand A Milk is 50% higher than the cost price. If it is sold at a price of $2.7 after applying a discount of 10% on the marked price, what is the profit % in selling Brand A milk?
A certain motorcycle company manufactured and sold each of its 1,200 motorcycles during the last fiscal year. Did the company make a profit on the sales of motorcycles?
(1) For each motorcycle sold, the company’s revenue was $10,000
(2) The company’s expenses comprise a fixed expense of $2,000,000 per quarter and an additional $3,500 for each motorcycle.
Sam bought a television set from a store at a discount of 10%. He sold the set to a friend at a further discount of 10%. What is the discount his friend got on the original list price of the television set?
A certain petroleum station purchased g gallons of petroleum for d dollars per gallon, and then it added e gallons of ethanol at f dollars per gallon. If this entire mixture were sold at h dollars per gallon, which of the following represents the gross profit per gallon on the sale of the mixture?
A certain electronics store purchased 500 tablets for $150 each. If it sold some at a 20% markup and the rest at a 40% markup, how many were sold at a 40% markup?
(1) Had the store sold all the tablets at a markup of 30%, its gross profit would have been 6.25% lower.
(2) The gross profit from the 40% lot were three times the gross profit from the 20% lot.
Jamie purchased three items from a budget store. She received discounts of 40% on the marked price of item A, 20% on the marked price of item B and 10% on the marked price of item C. How much money did she save, in percent terms, by shopping at the budget store?
(1) The marked price of item B is 75% of the marked price of item A and 200% more than the marked price of item C.
(2) The marked price of item A is 400% of the marked price of item C.
In 2012, the marked price of an electric vehicle was $50,000 and it was sold at a discount of n%. In early 2013, due to rise in fossil fuel prices, the demand for electric vehicles surged. Consequently, the price of the aforementioned electric vehicle was raised by m% over its earlier discounted price. What was the new selling price of the electric vehicle?
(1) m=10
(2) (100-n)(100+m)=2200
Stuart paid $60 for purchasing a pair of identical chairs. He decided to sell the chairs at a price equal to the purchase price plus a markup that is 40 percent of the marked price, set by him. When he could not sell the chairs for one day, he discounted their marked price by 20 percent and quickly sold one chair. Worrying that he had underpriced the chairs, he raised the marked price of the remaining chair by 20 percent and sold it by the end of the day. What was his total profit or loss for the combined transactions?
A dealer bought a merchandise at a% less than its marked price and then sold at b% less that its marked price. What was the value of the discount offered to customers?
(1) a = 6%
(2) The dealer made a profit of 5%
A furniture dealer purchased 10 sofas for $500 each. If he sells all the sofas for no more than $600 each, what is the lowest price that he can sell any of the sofas to earn an average gross profit of $90 per sofa?
If a material is sold for Rs. 34.80,Rs., there is a loss of 25%. Find out the cost price of the material?
|
93 videos|77 docs|104 tests
|
|
93 videos|77 docs|104 tests
|