Get the App Signup / Login
Sign in Open App

Test: Second Law of Thermodynamics & Entropy


20 Questions MCQ Test Topic-wise MCQ Tests for NEET | Test: Second Law of Thermodynamics & Entropy


Description
Attempt Test: Second Law of Thermodynamics & Entropy | 20 questions in 30 minutes | Mock test for NEET preparation | Free important questions MCQ to study Topic-wise MCQ Tests for NEET for NEET Exam | Download free PDF with solutions
QUESTION: 1

Direction (Q. Nos. 1-10) This section contains 10 multiple choice questions. Each question has four choices (a), (b), (c) and (d), out of which ONLY ONE option is correct.

Q. Entropy change for the following reversible process is 1 mole H2O

(l, 1 atm, 100°C ) 1 mole H2O (g , 1 atm, 100°C)(ΔHvap = 40850 J mol-1)

Solution:

∆S=Change in energy/Absolute temp =∆H/(100+273)K =40850/373 = 109.52 J/K/mol

QUESTION: 2

Entropy change when 2 moles of an ideal gas expands reversibly from an initial volume of 1 dm3 to a final volume of 10 dm3 at a constant temperature of 298 K is

Solution:

∆S= 2.303nR × log(V2/V1)Here n=2, R=8.314, V2= 10, V1= 1

QUESTION: 3

3 moles of a diatomic gas are heated from 127° C to 727° C at a constant pressure of 1 atm. Entropy change is (log 2.5 = 0 .4)

Solution:

∆S = nCplnT2/T1 + nRlnP1/P2
Since pressure is constant, so the second term will be zero.
Or ∆S = 3×7/2×8.314×2.303×log(1000/400)
= 80.42 JK-1

QUESTION: 4

10 dm3 of an ideal monoatomic gas at 27° C and 1.01 x 105 Nm-2 pressure are heated at constant pressure to 127°C. Thus entropy change is
Solution:

For isobaric process, we have ∆S =nCpln(T2/T1)
T2 = 273+127 = 400K and T1 = 273+227 = 300K
Applying pV = nRT at initial condition,
1×10 = n×0.0821×300
n = 0.40
Applying ∆S =nCpln(T2/T1)
∆S =0.40×5/2R×ln(400/300) = 2.38 JK-1

QUESTION: 5

Exactly 100 J of heat was transferred reversibly to a block of gold at 25.00° C from a thermal reservoir at 25.01 °C, and then exactly 100 J of heat was absorbed reversibled from the block of gold by a thermal reservoir at 24.99° C. Thus entropy change of the system is
Solution:
QUESTION: 6

Given

I. C (diamond) + O2(g) → CO2(g) ; ΔH° = - 91.0 kcdl mol-1
II. C(graphite) + O2(g) → CO2(g) ; ΔH° = - 94.0 kcal mol-1

Q. At 298 K, 2.4 kg of carbon (diamond) is converted into graphite form. Thus, entropy change is
Solution:

The reaction is 
C(diamond)     →     C(graphite)      ∆H = (94-91) = 3 kcal mol-1
∆S = ∆H/T
∆H = (94-91)×2.4×103/12   
= 600 kcal
∆S = 600/298 = 2.013 kcal K-1

QUESTION: 7

Consider a reversible isentropic expansion of 1.0 mole of an ideal monoatomic gas from 25°C to 75°C. If the initial pressure was 1.0 bar, final pressure is 
Solution:

Isentropic process means that entropy is constant. This is true only for reversible adiabatic process.
Applying P11-γ T1γ = P21-γ T2γ (for monatomic species, γ = 5/3)
(1/P)-⅔ = (75+273/25+273)5/3
Or (1/P)-2 = (348/298)5
Or P = 1.474 bar

QUESTION: 8

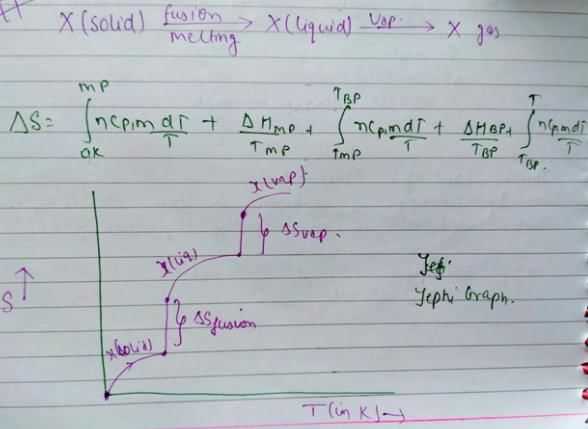
Consider the following figure representing the increase in entropy of a substance from absolute zero to its gaseous state at some temperature

Q. ΔS° (fusion) and ΔS° (vaporisation) are respectively indicated by 
Solution:


You  can co-relate both graph and the result will be option c.

QUESTION: 9

ΔHvap = 30 kJ mol-1 and ΔSvap = 75 J mol-1 K-1. Thus, temperature of the vapour at 1 atm is

[IIT JEE 2004]
Solution:

Vapour pressure is equal to atmospheric pressure ,it means the substance is at boiling point
At boiling point, liquid and Gas are in equilibrium. Therefore dG=0
dG = H - TdS
dG = 0
⇒H = TdS
⇒T = H/dS
⇒ T = 30 103/75 = 400K

QUESTION: 10

For the process, and 1 atmosphere pressure, the correct choice is

[JEE Advanced 2014]
Solution:

At 100°C and 1 atmosphere pressure H2O (l) ⇋ H2O(g) is at equilibrium. For equilibrium

*Multiple options can be correct
QUESTION: 11

Direction (Q. Nos. 11-14) This section contains 4 multiple choice questions. Each question has four choices (a), (b), (c) and (d), out of which ONE or  MORE THANT ONE  is correct.

Q. For an ideal gas, consider only (p -V) work in going from initial state X to the final state Z. The final state Z can be reached either of the two paths shown in the figure. Which of the following choice (s) is (are) correct?

(Take ΔS as change in entropy and W as work done)

[IIT JEE 2012]
Solution:

∆SX→Z = ∆SX→Y + ∆SY→Z(Entropy is a state function, so it is additive)
WX→Y→Z = WX→Y (work done in y→z is zero as the process is isochoric)

*Multiple options can be correct
QUESTION: 12

Benzene and naphthalene form an ideal solution at room temperature. For this process, the true statement(s) is (are)

[JEE Advanced 2013]
Solution:

When an ideal solution is formed process is spontaneous

According to Raoult's law, for an ideal solution

ΔH=0

ΔVmix​=0

Since there is no exchange of heat energy between system and surroundings

ΔSsurroundings​=0

ΔSsys.​=+ve

∴ From the relation

ΔG=ΔH–TΔS

ΔG=−ve

Hence, the correct options are B, C and D

*Multiple options can be correct
QUESTION: 13

Consider the following process

Select correct choices(s)
Solution:

∆SX→Y = ∆SX→Z + ∆SZ→Y(Entropy is a state function, so it is additive)
However, ∆SX→Z is zero. As for adiabatic process. There is no change in entropy. 
∆SX→Y =  ∆SZ→Y = 2.303 5 8.314 log(10/1) = 95.7 JK-1

*Multiple options can be correct
QUESTION: 14

In which of the following cases, entropy of I is larger than that of II?
Solution:

a) More molar mass, more entropy. So ∆SN2O4 > ∆SNO2
b) CO2 has more entropy than dry ice at -78°C
c) Pure alumina iss crystalline solid while ruby is amorphous. And ∆Samorphous > ∆SCrystalline. So alumina has less entropy than ruby.
d) At lower pressure, entropy be higher as gas particles are far from each other. So (∆SN2)1 bar > (∆SN2)5 bar 
 

QUESTION: 15

Direction (Q. Nos. 15 and 18) This section contains 2 paragraphs, each describing theory, experiments, data etc. Four questions related to the paragraphs have been given. Each question has only one correct answer among the four given options (a), (b), (c) and (d)

Passage I

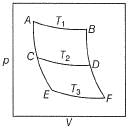
Consider a series of isotherms and adiabates as shown

AB, CD and EF are isotherms.
AC, CE, BD and D F are adiabates.

 

Q.

Solution:


AB, CD and EF are isotherms.
AC, CE, BD and D F are adiabates. 
For adiabatic process, we have change n entropy = 0
So EntropyA→B = EntropyC→D = EntropyE→F and EntropyA→C = EntropyA→C   = EntropyC→E = EntropyF→D = EntropyD→B
By this, all options are correct.  

QUESTION: 16

Passage I

Consider a series of isotherms and adiabates as shown

AB, CD and EF are isotherms.
AC, CE, BD and D F are adiabates.

 

Q. Select incorrect relationship

 
Solution:
QUESTION: 17

Passage II

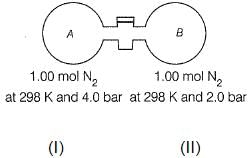
The stopcock connecting A and B is of negligible volume. Stopcock is opened and gases are allowed to mix isothermally.

 

Q. Final pressure set up is
Solution:


Volume in (I) = nRT/P1 = 1× 0.0821× 298/4 = 6.11 L
Volume in (II) = nRT/P2 = 1× 0.0821× 298/2 = 12.23 L
Total volume = 18.34 L
Applying PV = nRT at final condition, 
P = 2× 0.0821× 298/18.34 = 2.66

QUESTION: 18

Passage II

The stopcock connecting A and B is of negligible volume. Stopcock is opened and gases are allowed to mix isothermally.

 

Q. Entropy change for the system is 
Solution:
*Answer can only contain numeric values
QUESTION: 19

Direction (Q. Nos. 19 and 20) This section contains 2 questions. Each question, when worked out will result in an integer from 0 fo 9 (both inclusive).

Q. Consider two Carnot engines (1) and (2)

Efficiency η2
Derive the value of η2  η1

Solution:

η1 = 1-273/298 = 25/298
η2 = 1-248/298 = 50/298
η2/η1 = (50/298)/25/298 = 2

QUESTION: 20

A cyclic heat engine operates between a source temperature of 927 oC and a sink temperature of 27 oC. What will be the maximum efficiency of the heat engine?
Solution:

Heat engine is operated between the temperatures

T1 = 927 0C = 927 + 273 = 1200 K and
T2 = 27 0C = 27 + 273 = 300 K

The maximum efficiency of a heat engine is given by,

ηmax = 1 – (T2/T1)
ηmax = 1 – (300/1200)
ηmax = 0.75

Use Code STAYHOME200 and get INR 200 additional OFF
Use Coupon Code
Use Coupon Code

Recommended Content

Recommended Tests

How to Prepare for NEET

Read our guide to prepare for NEET which is created by Toppers & the best Teachers

Download free EduRev App

Track your progress, build streaks, highlight & save important lessons and more!
© EduRev
Follow Us