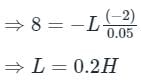Test: Self Inductance - 2 - Electronics and Communication Engineering (ECE) MCQ
10 Questions MCQ Test - Test: Self Inductance - 2
In a coil of N turns, a current of i produces a magnetic flux of ϕ. Find the self inductance of this coil.
Two inductors when connected in series with additive connection, their equivalent inductance is 400 µH and when same inductors connected in series with subtractive connection, their equivalent inductance is 300 µH. Find their mutual inductance.
If N is the number of turns in a coil, the value of self inductance varies as
A current in a coil of inductance 5 H decreases at a rate of 2 Amp/sec. The induced emf is
Current in a coil changes from 4 A to zero in 0.1 second and the emf induced is 100 V. The self inductance of the coil is
In a coil, the current changes from 4A to 2A in 0.05 sec. If the induced e.m.f. is 8 volt, then self-inductance of the coil is:
The self inductance of a long solenoid of length l is proportional to
When the current changes from +2A to -2A in 0.05 second, an emf of 8V is induced in the coil. The coefficient of self inductance of the coil is
A circuit possesses an inductance of 1 H when a current through coil is changing uniformly at the rate of 1 A/s inducing an opposing emf of 'X' volts in it.
What is the value of 'X'?
In a coil current changes from 2A to 4A in 0.05 second. If the average induced e.m.f. is 8 volt, then coefficient of self inductance is:


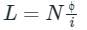


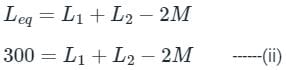

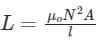
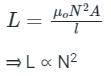
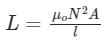

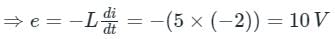
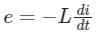
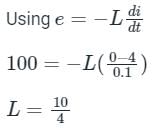
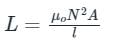
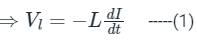

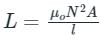
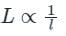

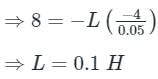
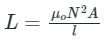
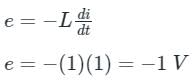
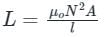
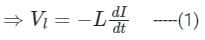 Where ,
Where ,