Test: Sets- 1 - Computer Science Engineering (CSE) MCQ
30 Questions MCQ Test - Test: Sets- 1
A binary operation  on a set of integers is defined as x
on a set of integers is defined as x  y = x2 + y2. Which one of the following statements is TRUE about
y = x2 + y2. Which one of the following statements is TRUE about  ?
?
 on a set of integers is defined as x
on a set of integers is defined as x  y = x2 + y2. Which one of the following statements is TRUE about
y = x2 + y2. Which one of the following statements is TRUE about  ?
?Consider the set S = {1, ω, ω2}, where ω and w2 are cube roots of unity. If * denotes the multiplication operation, the structure (S, *) forms
Which one of the following in NOT necessarily a property of a Group?
Consider the binary relation R = {(x, y), (x, z), (z, x), (z, y)} on the set {x, y, z}. Which one of the following is TRUE?
For the composition table of a cyclic group shown below
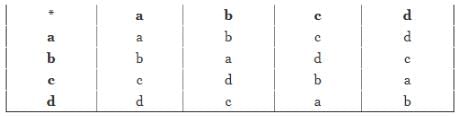
Q.
Which one of the following choices is correct?
Let S be a set of nelements. The number of ordered pairs in the largest and the smallest equivalence relations on S are:
How many different non-isomorphic Abelian groups of order 4 are there
Consider the set S = {a,b,c,d}. consider the following 4 partitions π1, π2, π3, π4 on S : π1 = 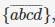 π2 =
π2 =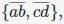 π3 =
π3 =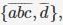 π4 =
π4 = 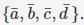 Let ρ be the partial order on the set of partitions S' = {π1,π2,π3, π4} defined as follows : πi ρ πj if and only if πi refines πj . The poset diagram for (S', ρ) is :
Let ρ be the partial order on the set of partitions S' = {π1,π2,π3, π4} defined as follows : πi ρ πj if and only if πi refines πj . The poset diagram for (S', ρ) is :
Consider the set of (column) vector defined by
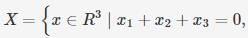
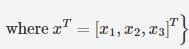
Which of the following is True ?
Let X, Y, Z be sets of sizes x, y and z respectively. Let W = X x Y. Let E be the set of all subsets of W. The number of functions from Z to E is:
The set {1, 2, 3, 5, 7, 8, 9} under multiplication modulo 10 is not a group. Given below are four plausible reasons. Which one of them is false?
A relation R is defined on ordered pairs of integers as follows: (x,y) R(u,v) if x < u and y > v. Then R is: Then R is:
Let S denote the set of all functions f: {0,1}4 -> {0,1}. Denote by N the number of functions from S to the set {0,1}.
Q.
The value of Log2Log2N is ______.
Consider the following relation on subsets of the set S of integers between 1 and 2014. For two distinct subsets U and V of S we say U < V if the minimum element in the symmetric difference of the two sets is in U. Consider the following two statements:
S1: There is a subset of S that is larger than every other subset.
S2: There is a subset of S that is smaller than every other subset.
Q. Which one of the following is CORRECT?
Let X and Y be finite sets and f: X -> Y be a function. Which one of the following statements is TRUE?
Let G be a group with 15 elements. Let L be a subgroup of G. It is known that L != G and that the size of L is at least 4.
Q. The size of L is __________.
If V1 and V2 are 4-dimensional subspaces of a 6-dimensional vector space V, then the smallest possible dimension of V1 ∩ V2 is ______.
There are two elements x, y in a group (G,∗) such that every element in the group can be written as a product of some number of x's and y's in some order. It is known that
x ∗ x = y ∗ y = x ∗ y ∗ x ∗ y = y ∗ x ∗ y ∗ x = e
Q.
where e is the identity element. The maximum number of elements in such a group is __________.
Consider the set of all functions f: {0,1, … ,2014} → {0,1, … ,2014} such that f(f(i)) = i, for all 0 ≤ i ≤ 2014. Consider the following statements:
P. For each such function it must be the case that for every i, f(i) = i.
Q. For each such function it must be the case that for some i, f(i) = i.
R. Each such function must be onto.
Q.
Which one of the following is CORRECT?
Let E, F and G be finite sets. Let X = (E ∩ F) - (F ∩ G) and Y = (E - (E ∩ G)) - (E - F). Which one of the following is true?
Given a set of elements N = {1, 2, ..., n} and two arbitrary subsets A⊆N and B⊆N, how many of the n! permutations π from N to N satisfy min(π(A)) = min(π(B)), where min(S) is the smallest integer in the set of integers S, and π(S) is the set of integers obtained by applying permutation π to each element of S?
Let S = {1,2,3, ....... , m}, m >3. Let X1 ...... Xn be subset of S each of size 3. Define a function f from S to the set of atural numbers as, f(i) is the number of sets Xj that contain the element i. That is 
Let A, B and C be non-empty sets and let X = (A - B) - C and Y = (A - C) - (B - C). Which one of the following is TRUE?
The following is the Hasse diagram of the poset [{a, b, c, d, e}, ≤]
The poset is
The set {1, 2, 4, 7, 8, 11, 13, 14} is a group under multiplication modulo 15. The inverses of 4 and 7 are respectively
Let R and S be any two equivalence relations on a non-empty set A. Which one of the following statements is TRUE?
Let f: B → C and g: A → B be two functions and let h = f o g. Given that h is an onto function. Which one of the following is TRUE?
What is the minimum number of ordered pairs of non-negative numbers that should be chosen to ensure that there are two pairs (a, b) and (c, d) in the chosen set such that "a ≡ c mod 3" and "b ≡ d mod 5"
Consider the binary relation:
S = {(x, y) | y = x+1 and x, y ∈ {0, 1, 2, ...}}
Q. The reflexive transitive closure of S is














