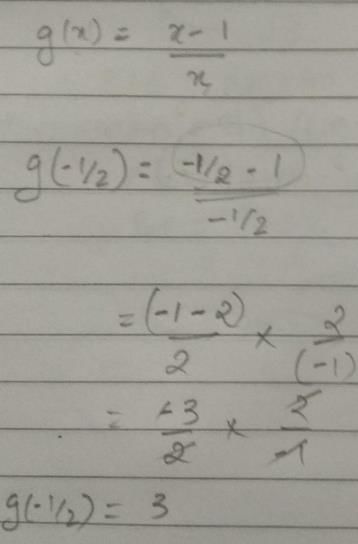Test: Sets- 2 - CA Foundation MCQ
30 Questions MCQ Test - Test: Sets- 2
The range of the function f(x) = log10(1 + x) for the domain of real values of x when 0 ≤ x ≤9 is
For the function h(x) = 101+x the domain of real values of x where 0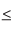 x
x 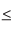 9 , the range is
9 , the range is
"is perpendicular to " over the set of straight lines in a given plane is
"is the reciprocal of" …….. over the set of non-zero real numbers is
If A has 32 elements, B has 42 elements and AUB has 62 elements, the number of elements in A ∩ B is
In a group of 20 children, 8 drink tea but not coffee and 13 like tea. The number of children drinking coffee but not tea is
The sets V = {x / x+2=0}, R={x / x2+2x=0} and S = {x : x2+x–2=0} are equal to one another if x is equal to
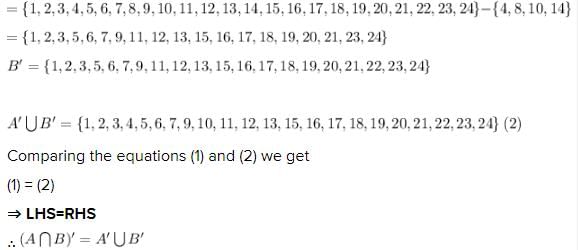
If the universal set E = {x |x is a positive integer <25} , A = {2, 6, 8, 14, 22}, B = {4, 8, 10, 14} then
If the set P has 3 elements, Q four and R two then the set P×Q×R contains
A town has a total population of 50,000. Out of it 28,000 read the newspaper X and 23000 read Y while 4000 read both the papers. The number of persons not reading X and Y both is
If A = { 1, 2, 3, 5, 7} and B = {1, 3, 6, 10, 15}. Cardinal number of A~B is
At a certain conference of 100 people there are 29 Indian women and 23 Indian men. Out of these Indian people 4 are doctors and 24 are either men or doctors. There are no foreign doctors. The number of women doctors attending the conference is