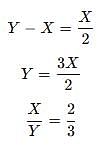Test: Sets- 2 - GMAT MCQ
25 Questions MCQ Test Quantitative for GMAT - Test: Sets- 2
If set A = {1, 3, 5, 7}, set B = {1, 4, 7}, find the value of A − B.
If the Cartesian product of two sets A and B(A × B) = {(3, 2), (3, 4), (5, 2), (5, 4)}, find set A.
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If A = {1, 3, 4} and B = {x : x ∈ R and x2 - 7x + 12 = 0} then which of the following is true ?
Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}. Then the number of subsets of A containing exactly two elements is
If A = {1, 2, 3, 4, 5, 7, 8, 9} and B = {2, 4, 6, 7, 9} then find the number of proper subsets of A ∩ B ?
If A = {1, 2, 5, 7} and B = {2, 4, 6} then find the number of proper subsets of A U B ?
In every (n + 1) - - elementic subset of the set (1, 2, 3, .......2n) which of the following is correct:
If A is a subset of B and B is a subset of C, then the cardinality of A ∪ B ∪ C is equal to:
In a survey of 1,000 consumers it is found that 720 consumers liked product A and 450 liked product B. What is the least number that must have liked both the products?
Consider the following statements:
1. A = {1, 3, 5} and B = {2, 4, 7} are equivalent sets.
2. A = {1, 5, 9} and B = {1, 5, 5, 9, 9} are equal sets.
Which of the above statements is/are correct?

The table above shows the research data gathered from a group of rural and urban residents. What is the number of rural residents who own a car?
(1) The number of rural residents in the group is 60% of the number of urban residents in the group.
(2) The difference between the number of urban residents who own a car and the number of rural residents who own a car is one-fifth of the number of rural and urban residents in the group.
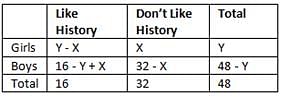
Of the 48 students in a class, 16 like to study History. What percentage of the girls in the class do not like to study History?
(1) One-third of the boys in the class like to study History
(2) The number of girls who like History is 50 percent of the number of girls who do not like History
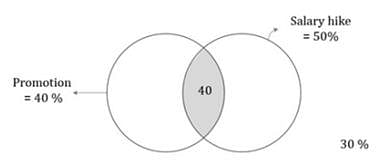
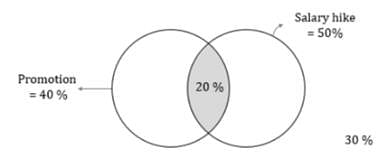
All the employees of Company X were appraised at the year end. 40% of the employees got a promotion, 50% of the employees got a salary hike and 30% of the employees neither got a promotion nor got a salary hike. If there were 40 employees who got both the promotion and the salary hike, what was the number of employees in the company?
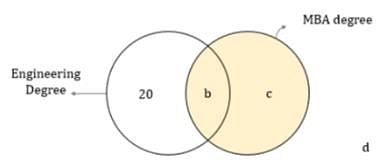
The human resources manager of a company compiled the data that the company had on the academic qualifications of its 100 employees. He observed that employees who had an Engineering and an MBA degree were the most in number and employees who had neither an Engineering nor an MBA degree were the least in number. If there were 20 employees who had an Engineering degree, but not an MBA degree, which of the following cannot be the number of employees who had an MBA degree?
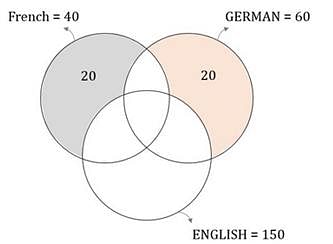
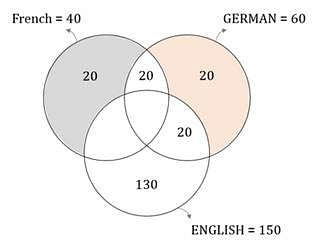
A survey was conducted to find out the number of languages spoken by the 210 employees of a company. It was found that 60 employees did not speak English, 150 employees did not speak German and 170 employees did not speak French. If there were 20 employees who did not speak German or English and 20 employees who did not speak French or English, what was the maximum number of employees who spoke only English? Assume that each of the employees spoke at least one language and no employee spoke any language other than English, French and German.
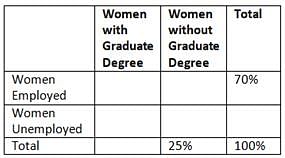
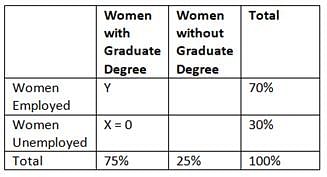
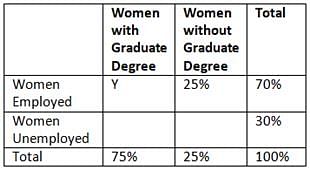
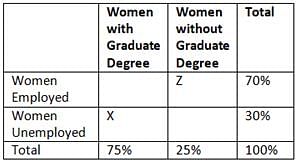
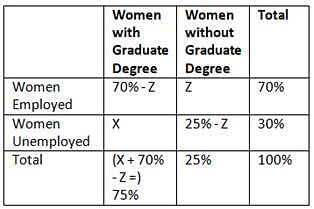
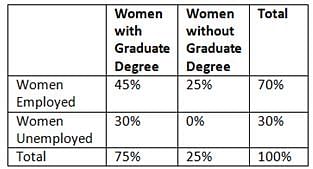
In a certain group of women, 70 percent of the women were employed and 25 percent did not have a graduate degree. Which of the following statements cannot be true?
- No woman in the group who had a graduate degree was unemployed
- Less than half of the women in the group were employed and had a graduate degree
- The number of unemployed women with a graduate degree was 50 percent greater than the number of employed women without a graduate degree
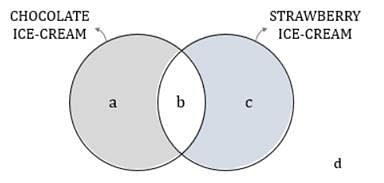
A group of friends went to an ice-cream parlour and ordered only two types of ice-cream - chocolate and strawberry. Of the people in the group, at least one person ate only one type ice-cream, some people ate both types of ice-cream and at least one person did not eat any type of ice-cream. Did more people eat chocolate ice-cream than strawberry ice-cream?
1) The ratio of the number of people who ate chocolate ice-cream and people who ate strawberry ice-cream was greater than the ratio of the total number of people who went to ice-cream parlour and the number of people who did not eat any type of ice-cream.
2) The number of people who ate only one type of ice-cream is greater than the number of people who ate strawberry ice-cream.
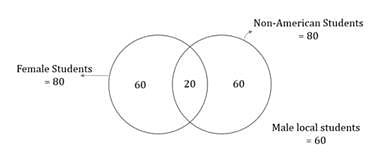
In College X in the United States, there are 200 students in a class, of which 80 are female. If 10% of the class consists of female non-American students and 3/5th of the class are American students, how many of the students in the class are male American students?
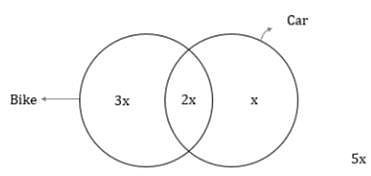
In a locality, for every person, who owns only a car, there are 3 people who own only a bike. The number of people who own both a car and a bike is half the number of people who either own only a car or only a bike. If the number of people who neither own a car nor a bike is equal to the number of people who own a bike, which of the following can be the total number of people in the locality?
In a certain class of 66 students, 30 students study Science, 40 students study Humanities and 40 students study Dance. If all the students studied at least one of the subjects, then what is the maximum possible number of students who study all the three subjects?
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|