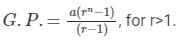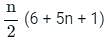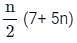Test: Sets and Sequences - ACT MCQ
15 Questions MCQ Test Mathematics for ACT - Test: Sets and Sequences
A person is to count 4500 currency notes. Let an denote the number of notes he counts in the nth minute. If a1 = a2 = .... = a10 = 150 and a10, a11 ...... are in an A.P. with common difference 2, then the time taken by him to count all notes is
The sum of 40 terms of an A.P. whose first term is 2 and common difference 4, will be
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
The third term of a G.P. is 9. The product of its first five terms is
The third term of a GP is 3. What is the product of the first five terms?
4th term of a G. P is 8 and 10th term is 27. Then its 6th term is?
The sum of (p + q)th and (p – q)th terms of an AP is equal to
If Tn = Tn - 1 + Tn - 2 , ∀ n ≥ 3 and T1 = 1 and T2 = 3 then T1 + T2 + T3 + T4 + T5 + T6 + T7 + T8 +T9 +T10 +T11 = ?
If nth term of a G.P. is 2n then find the sum of its first 6 terms.
Find the sum to n terms of the A.P., whose nth term is 5n + 1
The nth term of an A.P is 2+n/3, then the sum of first 97 terms is
If the numbers n - 3, 4n - 2, 5n + 1 are in AP, what is the value of n?
For what possible value of x are the numbers - 2/7, x, - 7/2 are in a GP ?
|
144 videos|100 docs|61 tests
|


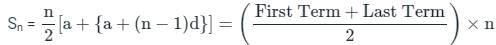
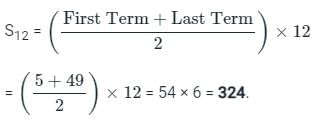
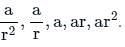

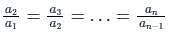
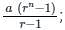 ; where r >1
; where r >1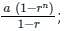 ; where r <1
; where r <1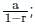 |r| < 1
|r| < 1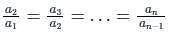
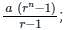 ; where r >1
; where r >1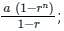 ; where r <1
; where r <1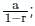 |r| < 1
|r| < 1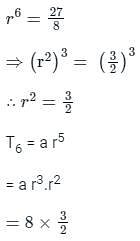
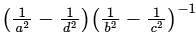 is
is