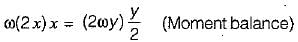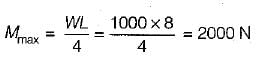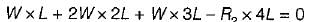Test: Shear Force & Bending Moment - 2 - Mechanical Engineering MCQ
10 Questions MCQ Test Topicwise Question Bank for Mechanical Engineering - Test: Shear Force & Bending Moment - 2
In a continuous curve of bending moment, the point of zero bending moment, where it changes sign is called
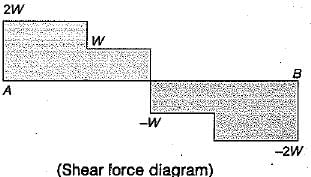
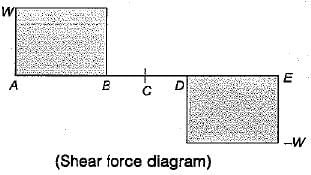
The beam is loaded as shown in figure. Select the correct BM diagram
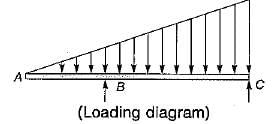

The structure shown in the figure below will be stable if
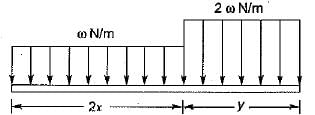

A beam 8 m long, simply supported at the ends, carries a point load of 1000 N at the mid-span. The bending moment under the load is
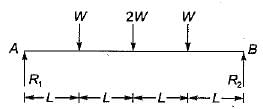
A simply supported beam is loaded as shown in the above figure below.
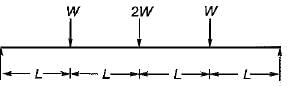
The maximum shear force in the beam will be
Which one of the following portions of the loaded beam shown in the given figure is subjected to pure bending?
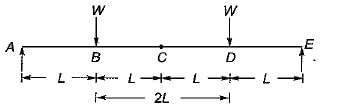
The point of contraflexure in a beam is at the location where the
The rate of change of bending moment is equal to
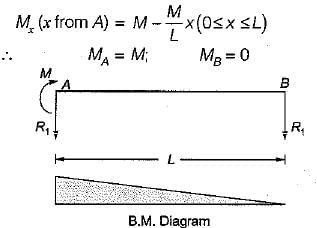
The BM diagram of the beam shown in figure is
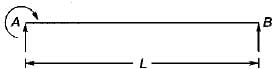
A cantilever carrying uniformly distributed load W over its full length is propped at its free end such that it is at the level of the fixed end. The bending moment will be zero at its free end and also at
|
45 videos|314 tests
|