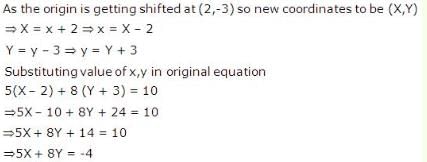Courses

Test: Shifting Of Origin


10 Questions MCQ Test Mathematics (Maths) Class 11 | Test: Shifting Of Origin


Description
This mock test of Test: Shifting Of Origin for JEE helps you for every JEE entrance exam. This contains 10 Multiple Choice Questions for JEE Test: Shifting Of Origin (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Shifting Of Origin quiz give you a good mix of easy questions and tough questions. JEE students definitely take this Test: Shifting Of Origin exercise for a better result in the exam. You can find other Test: Shifting Of Origin extra questions, long questions & short questions for JEE on EduRev as well by searching above.
QUESTION: 1

The origin lies on

Solution:

The origin lies on the intersection of X-axis and Y-axis. So, it lies on both the axes.

QUESTION: 2

What will be the new equation of the straight line 3x + 4y = 15, if the origin gets shifted to (1,-3) ?

Solution:

 Equation : 3x + 4y = 15
Points : (1,-3)
3(x-1) + 4(y+3) = 15
3x - 3 + 4y + 12 = 15
3x + 4y = 6

QUESTION: 3

What will be the new equation of the straight line 5x + 8y = 10, if the origin gets shifted to (2,-3) ?

Solution:

Equation : 5x + 8y = 10
Points (2, -3)
(x-2, y+3)
⇒ 5(x-2) + 8(y+3) = 10
= 5x - 10 + 8y + 24 = 10
⇒ 5x + 8 = - 4

QUESTION: 4

The point where all the angle bisectors of a triangle meet is
Solution:

The angle bisectors of the angles of a triangle are concurrent (they intersect in one common point). The point of concurrency of the angle bisectors is called the incenter of the triangle.

QUESTION: 5

What will be the new equation of the straight line 5x + 8y = 10, if the origin gets shifted to (2,-3) ?
Solution:
QUESTION: 6

What will be the value of ‘p” if the equation of the straight line 3x + 5y = 10 gets changed to 3x + 5y = p after shifting the origin at (2,2) ?
Solution:

3x + 5y = 10, at origin
But now, it’s (2,2),
3(x-2) + 5(y-2) = 10
Hence, 3x - 6 + 5y - 10 = 10
3x + 5y = 26
So, 3x + 5y = p
=> p = 26.

QUESTION: 7

If area of ΔABC = 0 ,three points A,B,C are
Solution:

The three points A, B and C are collinear if and only if area of ΔABC = 0.

QUESTION: 8

The distance between the pair of points (7,8) and (4,2) ,if origin is shifted to (1,-2) ,would be
Solution:
QUESTION: 9

The coordinates of centroid of triangle whose vertices are A(-1,-3), B(5,-6) and C(2,3) and origin gets shifted to (1,2) 
Solution:
QUESTION: 10

New coordinates of the point (7,-1) would be, if the origin is shifted to the point (1,2) by translation of the axis.
Solution:

 Let the new origin be (h, k) = (1, 2) and (x, y) = (7, -1) be the given point
Therefore new co-ordinates (X, Y) .
x = X + h and y = Y + k
i.e. 7 = X + 1 and -1 = Y + 2
This gives, X = 6 and Y = -3.
Thus the new co-ordinates are (6, -3)

Recommended Content

Recommended Tests

Similar Content

Related tests
Follow Us
© EduRev