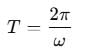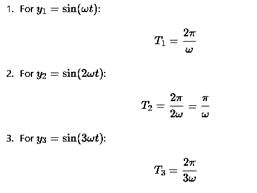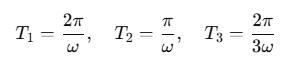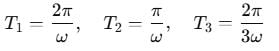Test: Simple Harmonic Motion
30 Questions MCQ Test Physics Class 11 | Test: Simple Harmonic Motion
| 1 Crore+ students have signed up on EduRev. Have you? |
Two identical spring, each of stiffness k are welded to each other at point P. The other two ends are fixed to the edge of a smooth horizontal tube as shown. A particle of mass m is welded at P. The entire system is horizontal. The period of oscillation of the particle in the direction of x is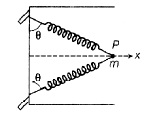 
Let us assume a force dF is applied at P in positive x - direction. This will stretch each spring by dl inducing a spring force dFs in each spring.
Let the static deformation of the system is dx (along the x-direction). The particle is in equilibrium. So,
Using Pythagoras theorem,
Here y is constant.
Two pendulums of length 100 cm and 121 cm starts oscillating. At some instant, the two are at the mean position in the same phase. After how many oscillations of the longer pendulum will the two be in the same phase at the mean position again
A pendulum has time period T for small oscillations. Now, an obstacle is situated below the
point of suspension O at a distance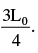 
The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
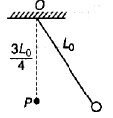
point of suspension O at a distance
The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position isFor the right (half) oscillation, 
For the left (half) oscillation, 
In the figure is shown a small block B of mass m resting on a smooth horizontal floor and the block is attached to an ideal spring (of force constant k). The spring is attached to vertical wall W1. At a distance d from the block, right side of it, is present the vertical wall W2. Now, the block is compressed by a distance 5d/3 and released. It starts oscillating. If the collision of the block with W2 are perfectly elastic, the time period of oscillation of the block is
absence of wall W2, the time period of block would have been 
But due to the presence of W2, it alters. But for the left part of oscillation (from the mean position shown), the period will be 
For the right side part, d = A sinω t [from x = A sinω t ]
This is the time taken by the block to reach W2 from mean position. Collision with W2 is perfectly elastic (given).
Time taken for right side part of oscillation will be
∴ Total time period is
Two simple pendulums of length 1m and 25 m, respectively, are both given small displacements in the same direction at the same instant.If they are in phase after the shorter pendulum has completed n oscillation, n is equal to
∴ T ∝ √L , as time period decreases when the length of pendulum decreases, the time period of shorter pendulum (Ts) is smaller than that of longer pendulum (Tl). That means shorter pendulum performs more oscillations in a given time.
It is given that after n oscillations of shorter pendulum, both are again in phase. So, by this time longer pendulum must have made (n – 1) oscillations.
So, the two pendulum shall be in the same phase for the first time when the shorter pendulum has
completed 5/4 oscillation
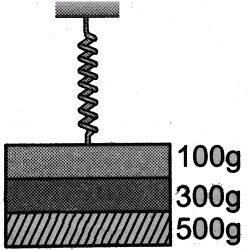
Three masses of 500 g, 300 g and 100 g are suspended at the end of an ideal spring as shown and are in equilibrium. When the 500 g mass is suddenly removed, the system oscillated with a period of 2 s. When 300 g mass is also removed, it will oscillate with the period
When 500 g is removed, m = (100 + 300)g = 0.4 kg
When 300 g is also removed,
A particle of mass m is executing oscillations about the origin on the X-axis with amplitude A. Its potential energy is given as U(x) = βx4 where β is a positive constant. The x- cordinate of the particle, when the potential energy is one- third of the kinetic energy, is
A linear harmonic oscillator of force constant 2 x 106 Nm–1 and amplitude 0.01 m has a total mechanical energy 160 J. Among the following statements, which are correct?
Total mechanical energy is 160
ET = J
∴ U max = 160 J
At extreme position KE is zero. Work done by spring force from extreme position to mean position is
The potential energy between two atoms in a diatomic molecule varies with x as 
where a and b are positive constants. Find the equivalent spring constant for
the oscillation of one atom if the other atom is kept
A particle of mass m moves in the potential energy U shown in the figure. The particle of the motion, if the total energy of the particle is Eo , is
For x<0
F = −dU/dx = −kx
ma = −kx
or a = −kx/m
−ω21x = −kx/m
ω1 = (√k/m)
T1 = 2π(√m/k)
For x>0 U = mgx
F = −dv/dx = −mg
But E = 1/2mv20
v0 = (√2E/m)
It is speed at lowest point
T2 = 2v0/g
= 2/g(√2E/m)
T = T1/2 + T2
= π(√m/k) + 2/g(√2E/m)
A particle of mass 0.1 kg is executing SHM of amplitude 0.1 m. When the particle passes through the mean position, its KE is 8 ×10-3 J. Find the equation of motion of the particle if the initial phase of oscillation is 45˚
According to question
By substituting the value we the final equation
The distance travelled by a particle executing SHM in 10 s, if the time period is 3 s, is
(It is given that the body starts from A√3/3 from equilibrium position, moves is positive direction at t = 0)
In 9s, the distance travelled = 4A × 3 = 12A
Imagine, now it is at
Two particles executing SHM with same angular frequency and amplitude A and 2A same
straight line with same position cross other in opposite direction at a distance A/3 from mean position. The phase difference between the two SHM’s is
Let particle (1) is moving towards right and particle (2) is moving towards left art this instant, 1 = 0
A spring-block pendulum is shown in the figure. The system is hanging in equilibrium. A bullet of mass m/2 moving with a speed u hits the block from down as shown in the figure. Find the amplitude of oscillation now.
In equilibrium position, mg = k x0
When the bullet gets embedded, the new equilibrium position changes. Let it is a distance x from initial equilibrium position.
Applying conservation of linear momentum,
So, at t = 0, mass 3m/2 is at a distance mg/2k from it mean position and moving up with velocity u/3
A particle at the end of a spring executes simple harmonic motion with a period T1 while the corresponding period for another spring is T2 If the period of oscillation with the two springs in series is T, then
A 7 kg disc is free to rotate about a horizontal axis passing through its centre O (see figure). The radius of the disc is 10 cm and spring constant of both the spring is 600 Nm-1 There is no slipping between the disc and the string. The time period of small oscillations of the disc is
When the angular displacement of the disc is θ the deformation (elongation and compression) in each spring is x = Rθ .
The displacement of the motion of a particle is represented (in metre) by the equation 
The motion of the particle is
∴ Amplitude is 0.4 m and motion is SHM.
A cylinder of radius r and mass m rests on a curved path of radius R as shown in the figure. It is slightly displaced to its left. Thus, the cylinder makes oscillation about the mean position. The period of oscillations is (the cylinder rolls without slipping)
The natural period of vibration of a 50 N disc (semicircular) is (The centre of mass of the semicircular disc lies at a distance of 4r/3π for the centre. Assume pure rolling).
Find the frequency of small oscillations of a thin uniform vertical rod of mass m and length L hinged at the point O as shown in the figure. The stiffness of each spring is k. Mass of the springs is negligible. The figure shows equilibrium position.
A uniform semicircular cylinder of radius R and mass m is displaced through a small angle
θ from its equilibrium position. It rolls without slipping during oscillations. The time period
of small oscillation is
Restoring torque is τ = mg ( O ' P ) = − I0 α
In the figure, θ is very small
A uniform disc of mass m and radius R is pivoted smoothly at P,.If a uniform thin ring of mass m and radius R is welded at the lower point of the disc, find the period of SHM of the system (disc + ring).
The time period of a physical pendulum is
where, I = MI of the system about point of sduspension
M = mass of the system and
l = distance between COM of the system and point suspension
Now, M = m + m = 2m
In the arrangement shows pulleys and spring are ideal. Now the block is slightly displaced vertically, the time period of oscillation is
In the figure shown pulley is massless. Initially the blocks are held at a height such that spring is in its natural length. The amplitude and velocity amplitude of block B1 respectively are (there is no slipping anywhere)
Decrease in GPE of B1 = Increase in Gravitational PE of B2 + Increase in elastic PE of spring.
Again applying law of conservation of mechanical energy at the mean position we get
The period of the function y = sinωt + sin2ωt + sin3ωt is
in time 
first function completes one oscillation, second function two oscillations and the third three
so for the combination T = 2π/ω
A plank of mass m is kept at rest on two identical sphere, each of mass mo and radius R The plank is connected to two ideal spring, which is turn are attached to walls as shown in the figure. Find the frequency of small (horizontal) oscillations (in the plane of the figure) of the plank. Assume pure rolling at all contact surfaces
Let the horizontal displacement of the plank, at an instant during its oscillation is x and its velocity is v.
A particle of mass m is allowed to oscillate on a smooth parabola x2 = 4ay, a > 0, about the origin O (see figure). For small oscillations, find the angular frequency ( ω )
During its oscillations, at a particular instant let the coordinates of the particle are (x, y) The total energy of the particle is
As oscillations are very small, we can ignore the middle term.
A solid uniform cylinder of mass m performs small oscillations in horizontal plane if slightly displaced from its mean position shown in the figure. Initially springs are in naturals and cylinder does not slip on ground during oscillations due to friction between ground and cylinder. Force constant of each spring is k. The time period of oscillation is
A snapshot during oscillations of the cylinder is shown in the figure. Its displacement is x and velocity v.
Its angular velocity is ω = V/R(Due to pure rolling)
As the centre of the cylinder is at a distance x from the initial position, the spring which are connected at a
point on its rim must be compressed and stretched by a distance 2x. Thus, at this intermediate position total
energy of the oscillation system can be given as
A particle of mass m is located in a unidimensional potential field, where the potential
energy of the particle depends on the coordinate x as 
where U0 and b are constant. Find the time period of small oscillations that the particle performs about the equilibrium position (solve the problem by Taylor’s method)
An air chamber of volume V, has a long neck of cross-sectional area A. A ball of mass m is fitted smoothly in the neck. The bulk modulus of air is B. If the ball is pressed down slightly and released, the time period of its oscillation is
Let the ball is pressed down by a small y, then the value of air decreased by Ay.
Then, excess pressure is
|
127 videos|464 docs|210 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
127 videos|464 docs|210 tests
|
How to Prepare for NEET
Download free EduRev App
Related content with Test: Simple Harmonic Motion
|
|
|
|
Related tests with Test: Simple Harmonic Motion
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
