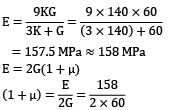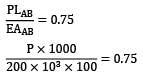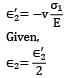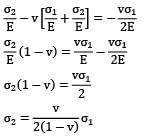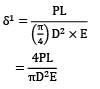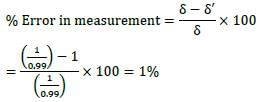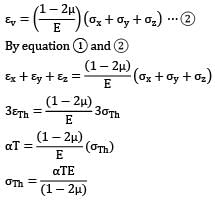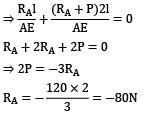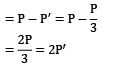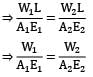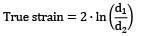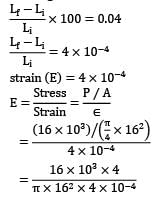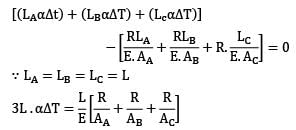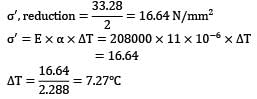Test: Simple Stress & Strain Level - 3 - Civil Engineering (CE) MCQ
20 Questions MCQ Test - Test: Simple Stress & Strain Level - 3
Consider the following statements Modulus of rigidity and bulk modulus of a material are found to be 60 GPa and 140 GPa respectively. Then
1. elasticity modulus is nearly 200 GPa
2. Poisson’s ratio is nearly 0.3
3. elasticity modulus is nearly 158 GPa
4. Poisson’s ratio is nearly 0.25
Which of these statements are correct?
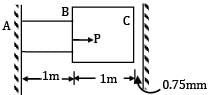
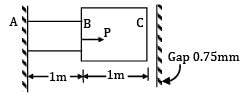
In the arrangement as shown in the figure, the stepped steel bar ABC is loaded by a load P. The material has Young’s modulus E = 200 GPa and the two portions AB and BC have area of cross section 1cm2 and 2cm2 respectively. The magnitude of load P required to fill up the gap of 0.75mm is

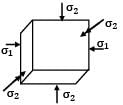
An elastic material of Young’s modulus E and Poisson’s ratio v is subjected to a compressive stress of σ1 in the longitudinal direction.
Suitable lateral compressive stress σ2 is also applied along the other two lateral directions to limit the net strain in each of the lateral directions to half of the magnitude that would be under σ1 acting alone. The magnitude of σ2 is
A spherical ball of a material of a diameter of 160mm goes down to a depth of 600 m in sea water. If the specific weight of sea water is 10.2kN/m3 and the bulk modulus of the material of the ball is 160kN/mm2, determine the change in volume of ball.
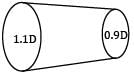
A bar of length L tapers uniformly from diameter 1.1 D at one end to 0.9 D at the other end. The elongation due to axial pull is computed using mean diameter D. What is the approximate error in computed elongation?
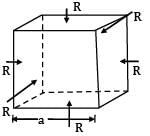
A cube having each side of length a, is constrained in all directions and is heated uniformly so that the temperature is raised by T℃ . If α is the thermal coefficient of expansion of the cube material and E the modulus of elasticity, the stress developed in the cube is
Consider the following statements: The thermal stress is induced in a component in general, when
1. a temperature gradient exists in the component
2. the component is free from any restraint
3. it is restrained to expand or contract freely
Which of the above statements are correct?
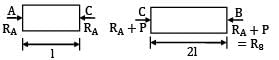
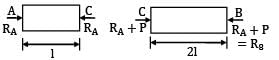
A straight bar is fixed at edges A and B. Its elastic modulus is E and cross-section is A. There is a load P = 120 N acting at C. Determine the reactions at the ends.
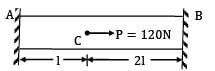
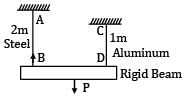
A rigid beam of negligible weight is supported in a horizontal position by two rods of steel and aluminum, 2m and 1m long having values of cross-sectional areas 1 cm2 and 2 cm2 and E of 200 GPa and 100 GPa respectively. A load P is applied as shown in the figure.
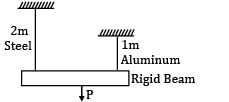
If the rigid beam is to remain horizontal then
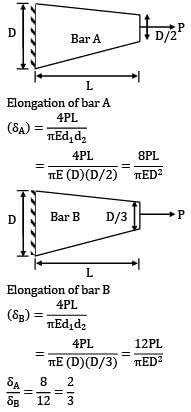
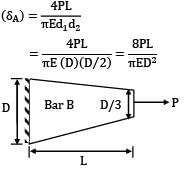
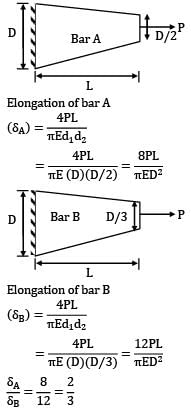
Two tapering bars of the same material are subjected to a tensile load P. The lengths of both the bars are the same. The larger diameter of each of the bars is D. The diameter of the bar A at its smaller end is D/2 and that of the bar b is D/3. What is the ratio of elongation of the bar A to that of the bar B?
For a composite bar consisting of a bar enclosed inside a tube of another material and when compressed under a load W as a whole through rigid plates at the end of the bar. The equation of compatibility is given by (Suffixes 1 and 2 refer to bar and tube respectively)
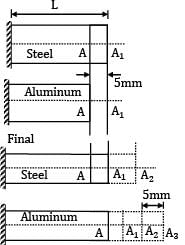
A tensile specimen with 12 mm initial diameter and 50 mm initial length is subjected to a load of 90 kN. After some time the diameter is 10 mm. Assuming it as incompressible material, Calculate the true strain along the length.
If the rigid rod fitted snugly between the supports as shown in the figure below, is heated, the stress induced in it due to 20℃ rise in temperature will be (α = 12.5 x 10-6/℃ E = 200GPa)
An aluminum bar of 8 m length and a steel bar of 5 mm longer in length are kept at 30℃.If the ambient temperature is raised gradually, at what temperature the aluminum bar will elongate 5 mm longer than the steel bar? (The linear expansion coefficients for steel and aluminum are 12 x 10−6/℃ and 23 x 10−6/℃ respectively)
A 16 mm diameter bar elongates by 0.04% under a tensile force of 16kN. The average decrease in diameter is found to be 0.01%. Then
1. E = 210 GPa and G = 77 GPa
2. E = 199 GPa and V = 0.25
3. E = 199 GPa and V = 0.30
4. E = 199 GPa and G = 80 GPa
Which of these values are correct?
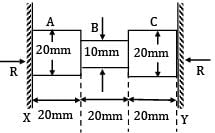
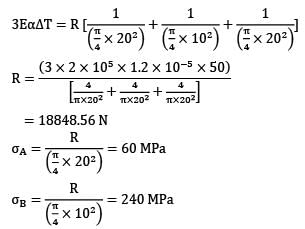
The figure shows a steel piece of diameter 20 mm at A and C, and 10 mm at B. the lengths of three sections A, B and C are each equal to 20 mm. The piece is held between two rigid surface x and Y. The coefficient of linear expansion α = 1.2 x 10−5 /℃ and Young’s Modulus E = 2 x 105 MPa for steel,
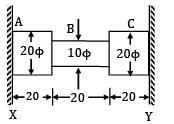
When the temperature of this piece increase by 50℃, the stresses in sections A and B are
A steel rod, 2 m long, is held between two walls and heated from 20℃ to 60℃. Young’s modulus and coefficient of linear expansion of rod material are 200 x 103 MPa and 10 x 10−6/℃ respectively. The stress induced in the rod, if walls yield by 0.2 mm, is
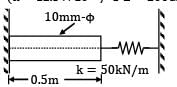
Two steel rods of 20 mm diameter are joined end to end by means of a turn buckle as shown in figure, other end of each rod is rigidly fixed. Initially, there is no tension in each rod. Effective length of each rod is 5 m. Threads on each rod has a pitch of 2.4 mm. Calculate the increase in tension when the turn buckle is tightened by one third of revolution. E = 208 GPa. If the temperature of the rods is increased, then at what temperature, tension in each rod is reduced to half of its magnitude. αs = 11 x 10−6/℃.

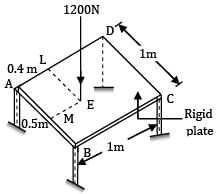
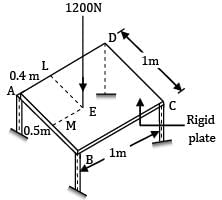
A rigid plate ABCD, 1 m2 is supported over four legs of equal lengths of same crosssection and same material. A vertical load 1200 N acts at point E such that
AM = LE = 0.5 m
AL = ME = 0.4 m
The reactions RA , RB , RC and RD are
A bar is subjected to tensile stresses of 100 MPa and 50 MPa in the direction x and y respectively. Strain produced in direction x is (Poisson's ratio = 0.5, E = 150 MPa)