Test: Single Correct MCQs: Circle | JEE Advanced - JEE MCQ
24 Questions MCQ Test - Test: Single Correct MCQs: Circle | JEE Advanced
A square is inscribed in the circle x2 + y2 – 2x + 4y + 3 = 0. Its sides are parallel to the coordinate axes. The one vertex of the square is (1980)
Two circles x2 + y2 = 6 and x2 + y2 – 6x + 8 = 0 are given. Then the equation of the circle through their points of intersection and the point (1, 1) is (1980)
The centre of the circle passing through the point (0, 1) and touching the curve y = x2 at (2, 4) is (1983 - 1 Mark)
The equation of the circle passing through (1, 1) and the points of intersection of x2 + y2 + 13x – 3y = 0 and 2x2 + 2y2 + 4x – 7y – 25 = 0 is (1983 - 1 Mark)
The locus of the mid -point of a chord of the circle x2 + y2 = 4 which subtends a right angle at the origin is (1984 - 2 Marks)
If a circle passes through the point (a, b) and cuts the circle x2 + y2 = k2 orthogonally, then the equation of the locus of its centre is (1988 - 2 Marks)
If the two circles (x – 1)2 + (y – 3)2 = r2 and x2 + y2 – 8x + 2y + 8 = 0 intersect in two distinct points, then (1989 - 2 Marks)
The lines 2x – 3y = 5 and 3x – 4y = 7 are diameters of a circle of area 154 sq. units. Then the equation of this circle is
The centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2 + y2 = 9 is (1992 - 2 Marks)
The locus of the centre of a circle, which touches externally the circle x2 + y2 – 6x – 6y + 14 = 0 and also touches the y-axis, is given by the equation: (1993 - 1 Marks)
The circles x2 + y2 – 10x + 16 = 0 and x2 + y2 = r2 intersect each other in two distinct points if (1994)
The angle between a pair of tangents drawn from a point P to the circle x2 + y2 + 4x – 6y + 9 sin2α + 13 cos2α = 0 is 2α.The equation of the locus of the point P is (1996 - 1 Mark)
If two distinct chords, drawn from the point (p, q) on the circle x2 + y2 = px + qy (where pq ≠ 0) are bisected by the x –axis, then (1999 - 2 Marks)
The triangle PQR is inscribed in the circle x2 + y2 = 25. If Q and R have co-ordinates (3,4) and (–4, 3) respectively, then ∠QPR is equal to (2000S)
If the circles x2 + y2 + 2x + 2ky + 6 = 0, x2 + y2 + 2ky + k = 0 intersect orthogonally, then k is (2000S)
Let AB be a chord of the circle x2 + y2 = r2 subtending a right angle at the centre. Then the locus of the centroid of the triangle PAB as P moves on the circle is (2001S)
Let PQ and RS be tangents at the extremities of the diameter PR of a circle of radius r. If PS and RQ intersect at a point X on the circumference of the circle, then 2r equals (2001S)
If the tangent at the point P on the circle x2 + y2 + 6x + 6y = 2 meets a straight line 5x –2y + 6 = 0 at a point Q on the y - axis, then the length of PQ is (2002S)
The centre of circle inscribed in square formed by the lines x2 – 8x + 12 = 0 and y2 – 14y + 45 = 0, is (2003S)
If one of the diameters of the circle x2 + y2 – 2x – 6y + 6 = 0 is a chord to the circle with centre (2, 1), then the radius of the circle is (2004S)
A circle is given by x2 + (y–1)2 = 1, another circle C touches it externally and also the x-axis, then the locus of its centre is (2005S)
Tangents drawn from the point P(1, 8) to the circle x2 + y2 –6x– 4y –11 = 0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is (2009)
The circle passing through the point (– 1, 0) and touching the y-axis at (0, 2) also passes through the point. (2011)
The locus of th e mid-point of the ch or d of con tact of tangents drawn from points lying on the straight line 4x – 5y = 20 to the circle x2 + y2 = 9 is (2012)






 i.e., 4x – y = 4
i.e., 4x – y = 4 = -1 ⇒ 4k = 18… (1)
= -1 ⇒ 4k = 18… (1) 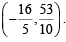







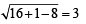

 and 5 > |r – 3 |
and 5 > |r – 3 |




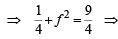




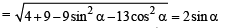




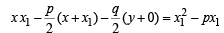 (using T = S1)
(using T = S1)




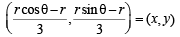

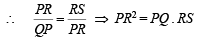











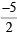





 ....(1)
....(1)
 and
and