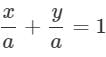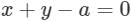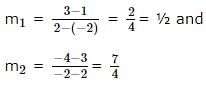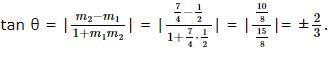Test: Slope Of A Line - Commerce MCQ
10 Questions MCQ Test Mathematics (Maths) Class 11 - Test: Slope Of A Line
The value of y, for the line passing through (3, y) and (2, 7) is parallel to the line passing through (-1 , 4) and (0, 6) is:
The tangent of the angle which the part of the line above the X-axis makes with the positive direction of the X-axis is:
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Two lines are said to be parallel when the difference of their slopes is:
Slope of a line which cuts intercepts of equal lengths on the axes is:
The points A and B have coordinates (3, 2) and (1, 4) respectively. So, the slope of any line perpendicular to AB is:
If the slope of the line passing through the points (2, 5) and (x, 1) is 2, then x = ______.
If the slope of line m = tan 0°. Therefore, the line is _____ to the X-axis.
If A (-2, 1), B (2, 3) and C (-2, -4) are three points, find the angle between the straight lines AB and BC.
Let A(2, 12) and B(6,4) be two points. The slope of a line perpendicular to the line AB is:
|
75 videos|238 docs|91 tests
|
|
75 videos|238 docs|91 tests
|