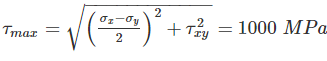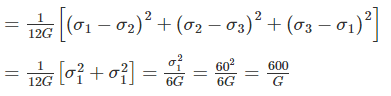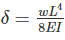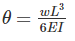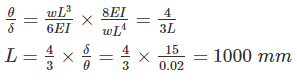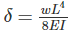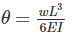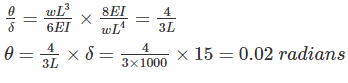Test: Solid Mechanics- 1 - SSC JE MCQ
20 Questions MCQ Test - Test: Solid Mechanics- 1
The maximum positive bending moment in a fixed beam of span 8m and subjected to a central point load of 120 kN is (in kN-m)
The major and minor principal stresses at a point are 3Mpa and -3Mpa respectively. The maximum shear stress at the point is
A point within the cross sectional plane of a beam through which the resultant of the external loading on the beam has to pass through to ensure pure bending without twisting of the cross-sectional of the beam is called:
A rectangular beam is 24 cm wide and 50 cm deep, its section modulus is given by:
The fixed support in a real beam becomes in the conjugate beam as:-
A simple supported beam with rectangular cross section is subjected to a concentrated load at mid span. If the width and depth of beam are doubled, the deflection at mid span will be reduced to:-
A tensile test is performed on a round bar. After fracture it has been found that the diameter remains approximately same at fracture. The material under test was
Consider the following statements:
1. On a Principal plane, only normal stress acts
2. On a Principal plane, both normal and shear stresses acts
3. On a Principal plane, only shear stress acts
4. Isotropic state of stress is independent of frame of reference
Which of the above statements is/are correct?
The ratio of crippling loads of a column having both the ends fixed to the column having both the ends hinged, is
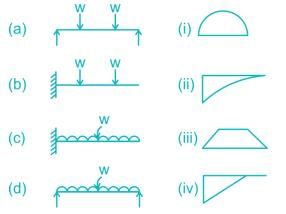
Match the following beams with their bending moment diagrams:
The crippling load taken by a column with both ends hinged is 100 kN. The crippling load taken by the same column with one end fixed and other end free will be:
Modulus of rigidity is defined as the ratio of ________.
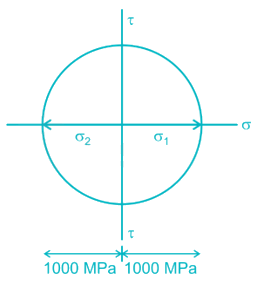
The Mohr’s circle given below corresponds to which one of the following stress condition.
If maximum principal stress σ1 = 60 N/mm2, σ2 and σ3 of value zero act on a cube of unit dimensions, then the maximum shear strain energy stored in it would be
If the deflection and slope at the free end of a cantilever beam subjected to the uniformly distributed load are 15 mm and 0.02 radians respectively. The length of the beam is _______.
The stress in a body due to suddenly applied load compared to when it is applied gradually is _______.
If the deflection at the free end of a cantilever beam of span 1 m, subjected UDL over entire span is 15 mm, then the slope at the free end is ________
For a given material, the modulus of rigidity is 120 GPa and Poisson’s ratio is 0.4. The value of modulus of elasticity in GPa is


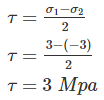

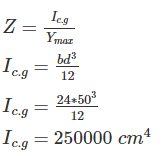
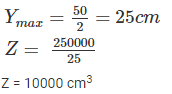

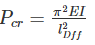
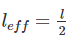
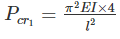
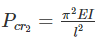
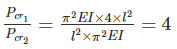
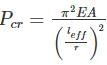
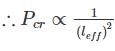 if all other parameters remain constant
if all other parameters remain constant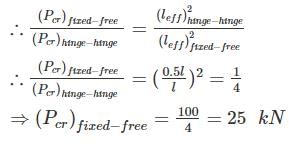
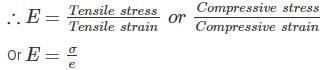
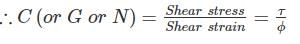
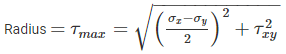
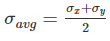 from the origin. Here it is in origin.
from the origin. Here it is in origin.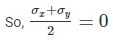
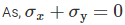 both the normal stress may be zero which is a pure shear case or opposite in nature which don’t exist in any of the options. So it is the pure shear case, where the radius is
both the normal stress may be zero which is a pure shear case or opposite in nature which don’t exist in any of the options. So it is the pure shear case, where the radius is