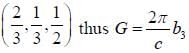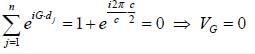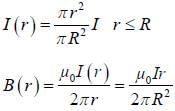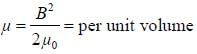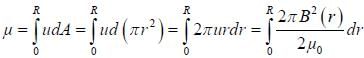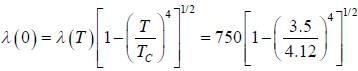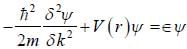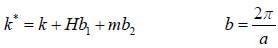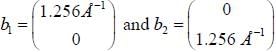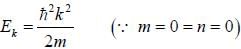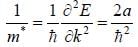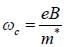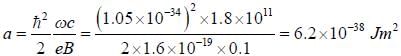Test: Solid State Physics - 2 - Physics MCQ
20 Questions MCQ Test GATE Physics Mock Test Series 2025 - Test: Solid State Physics - 2
A monoatomic. cubic material has lattice spacing of a. The sound velocity for longitudinal and transverse phonons is approximately equal. CT = CL = C, is isotropic. The debye frequency of the phonons will be
Graphite lias a layered crystal structure in which the coupling between carbon atoms in different lasers is much weaker than the atoms in the same layer. Using Debye theory, the specific heat is proportional to (where T is the temperature)
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
All X-ray beam of wavelength 1.7 Å is diffracted by a cubic KC1 ciystal of density 1.99 x 103 kg m-3. The interplance spacing for (200) planes and the glancing angle for the second order reflection from these planes will be (given that molecular weight of KC1 is 74.6 amu)
Elections of mass m are confined to one dimension. A weak periodic potential described by the fourier series
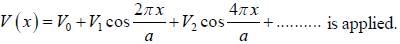
The energy gap (to first order) at 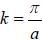 (between the first and second band is)
(between the first and second band is)
All electron of mass m moves in a square lattice of lattice spacing a. Assume that the nearly free electron approximation holds good. If there are two electrons per site, then which of the following is correct?
A paramagnetic substance lias 1028 atoms/m3. The magnetic moment of each atom is 1.8x10-23 Am2. Wliat would be the dipole moment of a bar of this material 0.1 meter long and 1 cnr cross-section placed in a field of 8x 104 Am-1?
A uniform silver wire has a resistivity of 1.54 x 10-8 Clm at room temperature and there are 5.8 x 1028 conduction electrons per m3. If an electric field of 1 volt cm is applied along the wire, the relaxation time of electron will be
Assuming that there are 1027 molecules /m3 in HCl vapour. The oiientation polarization at room temperature if the vapour is subjected to an electric field of 106 V/m will be (given that dipole moment of HCl molecule is 3.46x10-30 c-m)
Assume that the energy of the two particles in the field of each other is given by 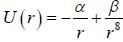 where
where
α and β are cosntants and r is the distance between the centres of paiticles. In stable configuration, the ratio of energy of attraction to the energy of repulsion will be____________(Answer should be an integer)
Sodium transforms frombcc to hep at about T = 23 K. Assumig that the density remains fixed and c/a ratio is
ideal. The hcp lattice spacing, a [given that the cubic lattice spacing a' = 4.23Å in the cubic phase] is_______Å (Answer should be upto two decimal places)
Atoms are arranged in a one-dimensional chain with lattice spacing a. Each atom is represented by the potential V(x) = 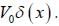 . The energy gaps between the bands, assuming that the nearly free electron approximation holds good, is
. The energy gaps between the bands, assuming that the nearly free electron approximation holds good, is
The effective mass tensor (Mij) for electrons in a simple cubic tight binding band at the centre (k = (0, 0,0) of the brillion zone will be
Consider a two dimensional hexagonal lattice if lattice spacing a = 3 Å and sound velocity c = 103 m/sec. The debye frequency, wD is (provide a numerical value in sec-1)
For a diatomic linear chain, the phonon dispersion relation ω (k) has two branches corresponding to + and - sign respectively
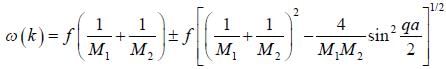
There are two atoms in the unit cell with masses and M2 and the force constant of nearest neighbour interaction is F and the effective mass 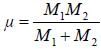 is kept constant. The velocity of sound will be
is kept constant. The velocity of sound will be
Consider a two dimensional square lattice with one atom of mass m per lattice point interacting with only nearest neighbours with force constant k. Take the phonon dispersion curve to be 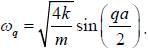 At high temperature
At high temperature 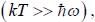 the mean square displacement of an atom from its equilibrium position will be
the mean square displacement of an atom from its equilibrium position will be
For a hexagonal closed packed structure with periodic potential 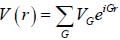 (G being a reciprocal lattice G
(G being a reciprocal lattice G
vector). If G corrosponding to the first brillion zone face in the C direction C that is normal to the face is in the (001) direction), then the value of VG is
A type-II superconducting wire of radius R carries current uniformly through its cross-section. If die total current earned by the wire is I. the magnetic energy per unit length of the wire is I. the magnetic energy per unit length of the wire is
The penetrating depth of mercury at 3.5 k is about 750 Å. The penetration depth at OK will be
Consider two dimensional electrons subjected to a weak periodic potential coming from a square lattice of spacing a = 5Å. For k vectors for away from the bu llion zone boundaries, the wavefunctions can be well
described by plane waves. Assume we want to write the wavefunction in block form, . Consider a state of energy E and wavevector
. Consider a state of energy E and wavevector 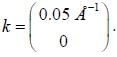 The lowest energy at this wave number will be ________________eV (upto second decimal places)
The lowest energy at this wave number will be ________________eV (upto second decimal places)
Assume that the E vs k relationship for electrons in the conduction band of a hypothetical tetravalent n-type semiconductor can be approximated by E = ak2 + constant. The cyclotron resonane for electrons in a field B = 0.1 Weber/m2 occurs at an angular frequency ωe = 1.8 x 1011 rad s-1The value of a is_______x 10-38(in the untis of Jm2)
|
1 docs|34 tests
|


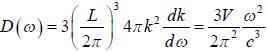
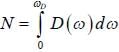
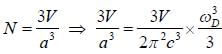
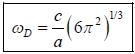
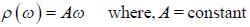
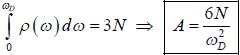
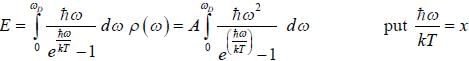
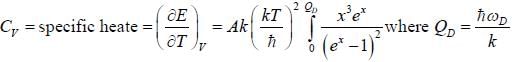
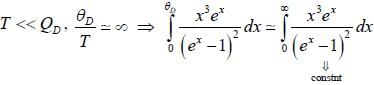
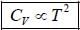
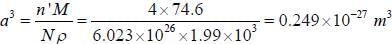
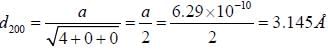
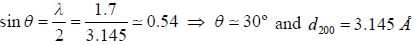
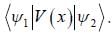 Iii the neighbourhood of k
Iii the neighbourhood of k  (for lower band) and
(for lower band) and 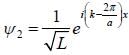 or the upper band L is the length of sys te m ψ1 and ψ2 are calculated using extended zone
or the upper band L is the length of sys te m ψ1 and ψ2 are calculated using extended zone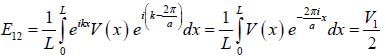
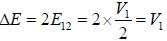
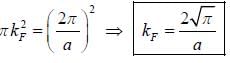
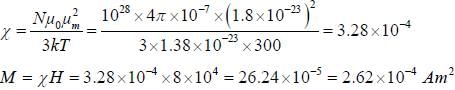
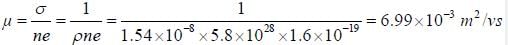
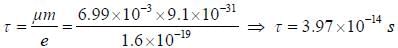
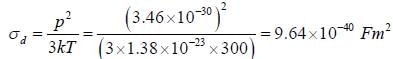
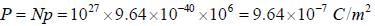
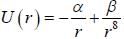
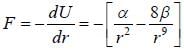
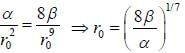
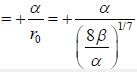
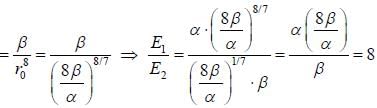
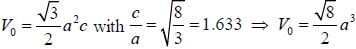
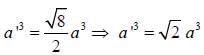

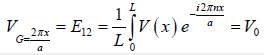
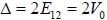
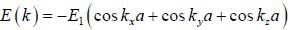
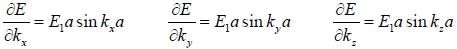
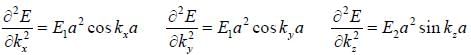
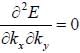
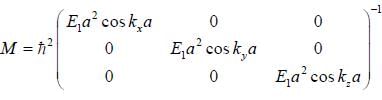
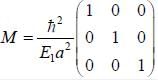
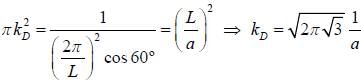
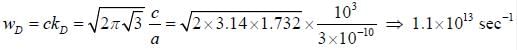
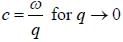
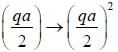
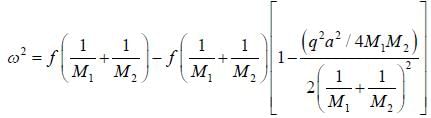
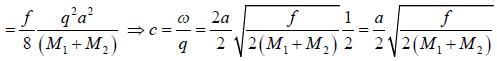
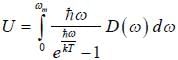
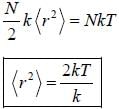
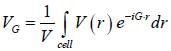
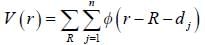
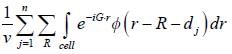
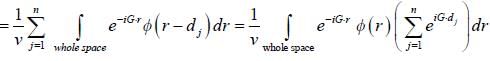
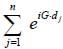 is the geomatric structure factor
is the geomatric structure factor