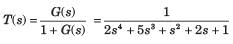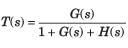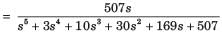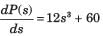Test: Stability - Electronics and Communication Engineering (ECE) MCQ
15 Questions MCQ Test - Test: Stability
The forward-path transfer function of a ufb system is

For system to be stable, the range of K is
The open-loop transfer function of a ufb system is


The closed loop system will be stable if the value of K is


The poles location for this system is shown in fig.The value of K is

The forward-path transfer function of a ufb system is T(s) = 
The system is
The open loop transfer function of a system is as
The range of K for stable system will be
The open-loop transfer function of a ufb control system is given by

For the system to be stable the range of K is
If the roots have negative real parts, then the response is ____________
The closed loop transfer function of a system is
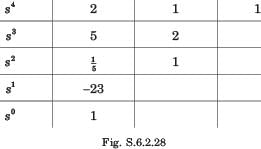
The number of poles in RHP and in LHP are
The closed loop transfer function of a system is
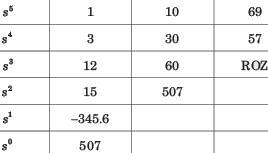
The number of poles in LHP, in RHP, and on jω - axis are
For the system shown in fig. the number of poles on RHP, LHP, and imaginary axis areS
For the open loop system of fig. location of poles on RHP, LHP, and an jω - axis are







 satisfy this condition.
satisfy this condition.
 Then apply feedback formula with
Then apply feedback formula with  and
and  and then multiply with s2.
and then multiply with s2.