Test: Standard Deviation - GMAT MCQ
10 Questions MCQ Test - Test: Standard Deviation
Set A consists of all prime numbers between 10 and 25; Set B consists of consecutive even integers, and set C consists of consecutive multiples of 7. If all the three sets have an equal number of terms, which of the following represents the ranking of these sets in an ascending order of the standard deviation?
Set A consists of all even integers between 2 and 100, inclusive. Set X is derived by reducing each term in set A by 50, set Y is derived by multiplying each term in set A by 1.5, and set Z is derived by dividing each term in set A by -4. Which of the following represents the ranking of the three sets in descending order of standard deviation?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If M is a negative integer and K is a positive integer, which of the following could be the standard deviation of a set {-7, -5, -3, M, 0, 1, 3, K, 7}?
I. -1.5
II. -2
III. 0
I. -1.5
II. -2
III. 0
Sets A, B and C are shown below. If number 100 is included in each of these sets, which of the following represents the correct ordering of the sets in terms of the absolute increase in their standard deviation, from largest to smallest?
A {30, 50, 70, 90, 110},
B {-20, -10, 0, 10, 20},
C {30, 35, 40, 45, 50}
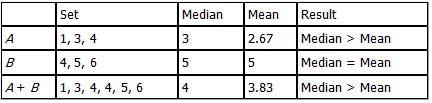
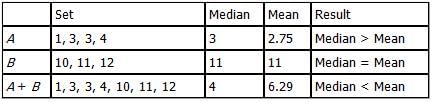
The table below represents three sets of numbers with their respective medians, means and standard
deviations. The third set, Set [A+B], denotes the set that is formed by combining Set A and Set B.
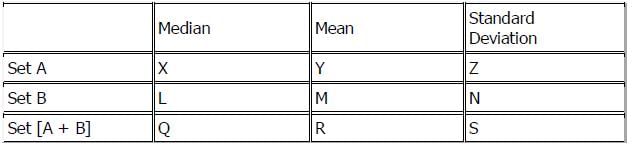
If X – Y > 0 and L – M = 0, then which of the following must be true?
I. Z > N II. R > M III. Q > R
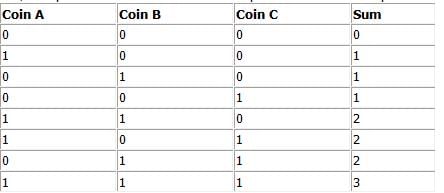
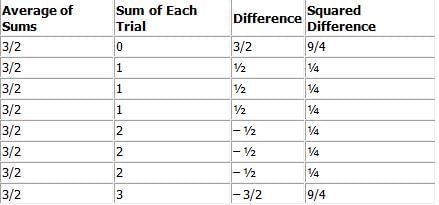
Three fair coins are labeled with a zero (0) on one side and a one (1) on the other side. Jimmy flips all three coins at once and computes the sum of the numbers displayed. He does this over 1000 times, writing downthe sums in a long list. What is the expected standard deviation of the sums on this list?
Let Set T = {2, 4, 5, 7}. Which of the following values, if added to Set T, would most increase the standard deviation of Set T?
9.4, 9.9, 9.9, 9.9, 10.0, 10.2, 10.2, 10.5
The mean and the standard deviation of the 8 numbers shown are 10 and 0.3, respectively. What percentageof the 8 number's are within 1 standard deviation?
70, 75,80,85,90,105,105,130,130,130
The list shown consists of the times, in seconds, that i took each of 10 schoolchildren to run a distance of 400 on of meters. If the standard devastation of the 10 running times is 22.4 seconds, rounded to the nearest tenth of a second, how many of the 10 running times are more than 1 standard deviation below the mean of the 10 running times?
The residents of town x participated in a survey to determine the number of hours per week each resident spent watching television. The distribution of the result of the survey had a mean of 21 hours and a standarddeviation of 6 hours. The number of hours of that participated, a resident of town x watching television lastweek was between 1 and 2 standard deviations below the mean. Which of the following could be the numberof hours the participated watched television last week?