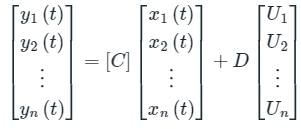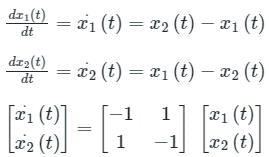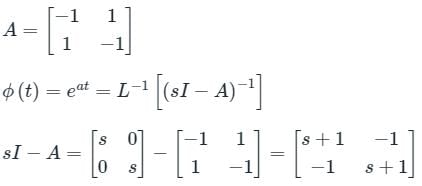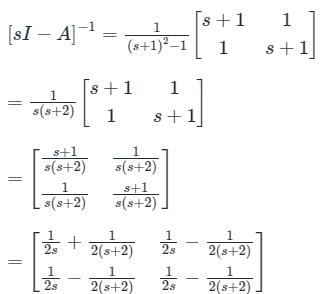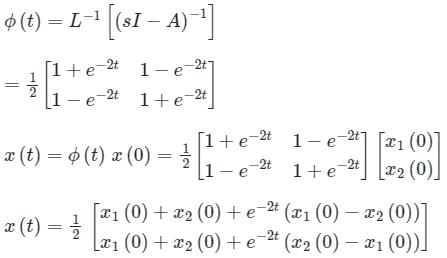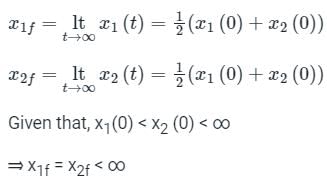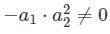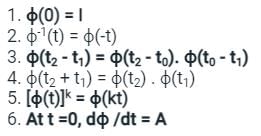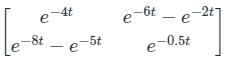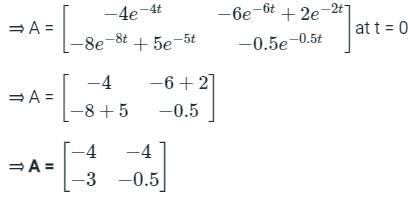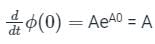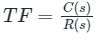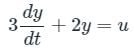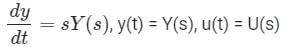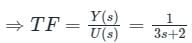Test: State Space Analysis - Electrical Engineering (EE) MCQ
10 Questions MCQ Test - Test: State Space Analysis
Which of the following properties are associated with the state transition matrix ϕ(t)?
1. ϕ(0) = I
2. ϕ(t2 - t1) = ϕ(t2) . ϕ-1(t1)
3. ϕ(t2 + t1) = ϕ(t2) . ϕ(t1)
4. ϕ(t2 - t1) = ϕ(t2 - t0). ϕ(t0 - t1)
Select the correct answer using the codes given below:
1. ϕ(0) = I
2. ϕ(t2 - t1) = ϕ(t2) . ϕ-1(t1)
3. ϕ(t2 + t1) = ϕ(t2) . ϕ(t1)
4. ϕ(t2 - t1) = ϕ(t2 - t0). ϕ(t0 - t1)
Select the correct answer using the codes given below:
Read the statements regarding controllability and observability and mark the answer as true and false.
- For a system to be controllable, |Qc| = 0.
- For the system to be observable, |Q0| = 0.
- For the system to be controllable and observable, |Qc| ≠ 0 and |Qo| ≠ 0.
The transfer function G(S) = C(SI - A)-1b of the system
x' = Ax + bu
y = Cx + du
has no pole-zero cancellation. The system
x' = Ax + bu
y = Cx + du
has no pole-zero cancellation. The system
Which of the following can be extended to time-varying systems?
Consider a system governed by the following equations
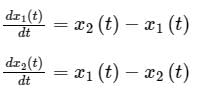
The initial conditions are such that 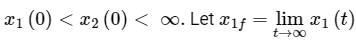 and
and  Which one of the following is true?
Which one of the following is true?
State variable description of an LTI system is given by
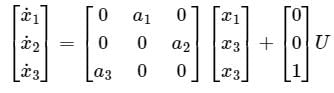
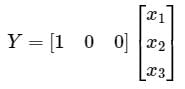
Where Y is the output and u is input. System is controllable for
The state transition matrix of a control system is 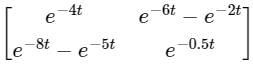 . The system matrix A is
. The system matrix A is
Consider the following properties attributed to state model of a system:
- State model is unique.
- Transfer function for the system is unique.
- State model can be derived from transfer function of the system.
Which of the above statements are correct?
The linear time invariant system is represented by the state space model as
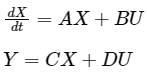
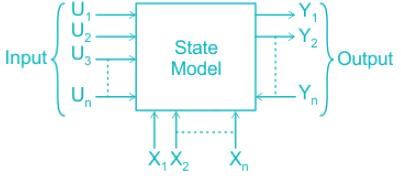
Consider n=number of state variables, m = number of inputs, p= number of outputs. The state transition matrix Φ( t) Φ( t) is given by:
A system is represented by 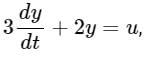 what is the transfer function to the system?
what is the transfer function to the system?