Test: Statistics- 2 - GMAT MCQ
20 Questions MCQ Test Quantitative for GMAT - Test: Statistics- 2
The numbers in set P denote the distance of certain positive integers from -1 on the number line. The numbers in set Q denote
the distance of the same integers from 1 on the number line. Which of the following statements is true about the standard deviation of the sets P and Q?
the distance of the same integers from 1 on the number line. Which of the following statements is true about the standard deviation of the sets P and Q?
List A: 20, 4, 8, x
List B: 8, 3, 6, 12, -4
List A above has 4 numbers and List B above has 5 numbers. What is the value of x?
(1) The range of the numbers in List A is equal to the range of the numbers in List B
(2) The median of the numbers in List A is equal to the median of the numbers in List B.
List B: 8, 3, 6, 12, -4
List A above has 4 numbers and List B above has 5 numbers. What is the value of x?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
When positive integer y is added to each of the first n non-negative integers, which of the following statements is true?
I. If the median of the resulting numbers is 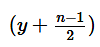 then n is odd
then n is odd
II. The arithmetic mean of the resulting numbers is equal to the median of the resulting numbers
III. The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.
I. If the median of the resulting numbers is
III. The arithmetic mean of the resulting numbers is y units greater than the arithmetic mean of the first n positive integers.
If a, b and c are positive integers, what is the average (arithmetic mean) of a and c?
1. The average of a + b and 4 is 6
2. The average of a + c and b is 18
In an inter-state Mathematics Olympiad, the distribution of the scores obtained by the participating students is symmetric about
the mean m. 68 percent of the distribution lies within one standard deviation d of the mean and 95 percent of the distribution lies
within 2 standard deviations of the mean. If there were 70 students who scored more than Ricky, 428 students who scored less than Ricky and none that scored equal to him, his score must lie between
The average (arithmetic mean) of the prime numbers that lie between 10 and 20 is how much greater than the average of the
prime numbers that lie between 1 and 10?
A group of students was participating in a quizzing competition consisting of 3 rounds. A student had to clear the first round to move into the second round and so on till he cleared all the rounds. What was the median number of the rounds cleared by the students in the quiz?
(1) 20 percent of the students could not clear round 1 of the quiz
(2) 40 percent of the students could clear round 2 but could not clear round 3.
Arrange the following sets in the order of the increasing magnitude of their mean to standard deviation ratio.
I. {50, 60, 70, 80}
II. {35, 40, 45, 50}
III. {90, 110, 130, 150}
Set P has n integers. What is the standard deviation of Set P?
(1) The range of Set P is equal to zero
(2) The mean of Set P is equal to the median of Set P
In triangle ABC (not shown), is the range of the angles of the triangle greater than 90o?
(1) The median angle of triangle ABC is 70o
(2) The difference between the two larger angles of triangle ABC
is 10o
Set P consists of 10 positive integers arranged in order of increasing magnitude. The difference between any two successive
terms of the set is 4. If the two largest terms of the set are removed, what is the decrease in the average(arithmetic mean) of
the set?
A is the average (arithmetic mean) of the first 7 multiples of 3 and B is the median of the first 3 multiples of positive integer n. If the
value of A2 – B2 is zero, what is the value of n?
Set P contains 3 distinct positive integers: A, B and C. Is the average (arithmetic mean) of set P divisible by 3?
(1) The sum of A×104 , B×102 and C is divisible by 9
(2) The product of the range of Set P and the median of Set P is 18.
A set consists of n distinct integers arranged in the order of increasing magnitude. Is the median of the n integers equal to the
arithmetic mean of the n integers?
(1) The sum of any 3 successive integers of the set is divisible by 3
(2) The difference between any 2 successive integers of the set is 4
Set A consists of 15 positive integers. Is the mean of set A equal to the median of set A?
(1) The integers in set A, when arranged in the order of increasing magnitude, are not evenly spaced
(2) If an integer x, which is equal to the mean of set A, is added to the set, the median of the set does not
change
A merchant sold 32 antique items for $28800. If his profit margin was 20%, then his average cost per antique item was
List A contains 16 distinct odd integers and 9 distinct even integers such that the average (arithmetic mean) of List A is 13.84. If each odd integer is doubled in magnitude, what is the new average (arithmetic mean) of List A?
(1) The average (arithmetic mean) of the even integers in List A is 10
(2) Before each odd integer is doubled in magnitude, the smallest odd integer in List A is 1 and the largest odd integer in List A is
31.
While debugging a piece of software, an engineer records the number of bugs he finds each day. If the number of bugs found by the engineer reduces by x with each passing day, what is the standard deviation of the number of bugs found by the engineer during the last 7 days?
(1) The difference between the maximum number of bugs and the minimum number of bugs found by the engineer during the last 7
days is 24.
(2) The average (arithmetic mean) number of bugs found by the engineer during the last 7 days is 24
A group of 4 boys and 5 girls take a test. What is the average (arithmetic mean) score of the group in the test?
- The average score of the boys is 23 points while the average score of the girls is 20 points
- If one of the girls had scored 6 points more, the average score of the group would have been 22
The table above shows the distribution of the distance, rounded to the nearest integer, run by 20 athletes in a marathon. Which of the
following cannot be the approximate average (arithmetic mean) distance run (in kilometres) by the athletes in the marathon?
|
115 videos|106 docs|113 tests
|
|
115 videos|106 docs|113 tests
|

















