Test: Statistics- 3 - GMAT MCQ
10 Questions MCQ Test - Test: Statistics- 3
If the mean of numbers 28, x, 42, 78 and 104 is 62, what is the mean of 48, 62, 98, 124 and x?
The arithmetic mean of the 5 consecutive integers starting with 's' is 'a'. What is the arithmetic mean of 9 consecutive integers that start with s + 2?
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
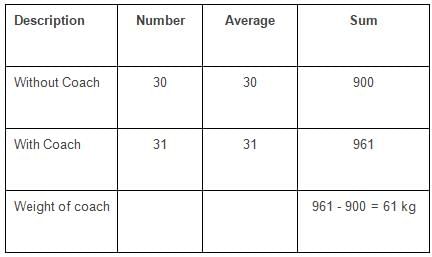
The average weight of a group of 30 friends increases by 1 kg when the weight of their football coach was added. If average weight of the group after including the weight of the football coach is 31 kg, what is the weight of their football coach?
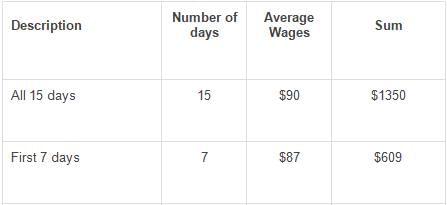
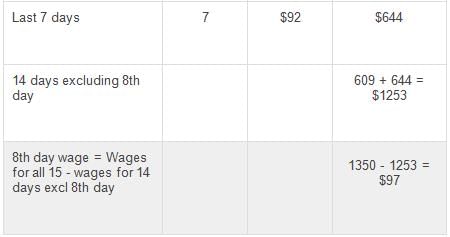
The average wages of a worker during a fortnight comprising 15 consecutive working days was $90 per day. During the first 7 days, his average wages was $87/day and the average wages during the last 7 days was $92 /day. What was his wage on the 8th day?
The average of 5 quantities is 6. The average of 3 of them is 8. What is the average of the remaining two numbers?
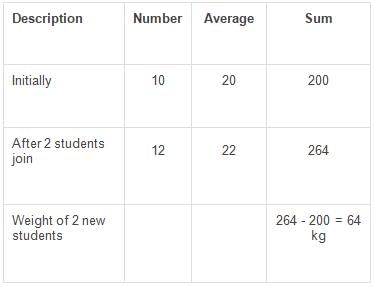
The average age of a group of 10 students was 20. The average age increased by 2 years when two new students joined the group. What is the average age of the two new students who joined the group?
Positive integers from 1 to 45, inclusive are placed in 5 groups of 9 each. What is the highest possible average of the medians of these 5 groups?
If the average of 5 positive integers is 40 and the difference between the largest and the smallest of these 5 numbers is 10, what is the maximum value possible for the largest of these 5 integers?
An analysis of the monthly incentives received by 5 salesmen : The mean and median of the incentives is $7000. The only mode among the observations is $12,000. Incentives paid to each salesman were in full thousands. What is the difference between the highest and the lowest incentive received by the 5 salesmen in the month?
Data Sufficiency:
If m, s are the average and standard deviation of integers a, b, c, and d, is s > 0?
- m > a
- a + b + c + d = 0