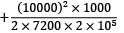Test: Strain Energy And Resilience Level - 3 - Civil Engineering (CE) MCQ
10 Questions MCQ Test - Test: Strain Energy And Resilience Level - 3
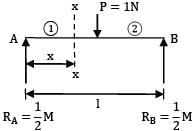
A simply supported beam of span ‘l’ and flexural rigidity EI carries a unit load at its mid-span section; the strain energy of the beam is
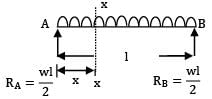
A simply supported beam of span l carries a uniformly distributed load w/m over the entire span; the strain energy of the beam is given by
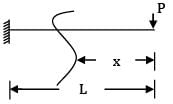
The strain energy of stored due to bending for cantilever beam of span L, modulus of elasticity E, moment of inertia I and a point load P at the free end is
Total strain energy stored in a simply supported beam of span, 'L' and flexural rigidity 'EI 'subjected to a concentrated load 'W' at the centre is equal to
A steel specimen 150 mm2 in cross-section stretches by 0 · 05 mm over a 50 mm gauge length under an axial load of 30 kN. What is the strain energy stored in the specimen? (Take E = 200 GPa)
A cantilever beam, 2 m in length, is subjected to a uniformly distributed load of 5 kN/m. If E = 200 GPa and I = 1000 cm4, the strain energy stored in the beam will be
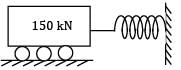
A truck weighing 150 kN and travelling at 2 m/sec impacts with a buffer spring which compresses 1.25 cm per 10 kN. The maximum compression of the spring is
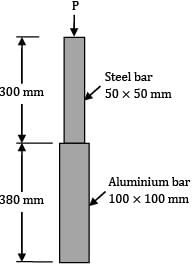
A member formed by connecting a steel bar to an aluminium bar is shown in figure. Assuming that the bars are prevented from bucking sidewise, calculate the magnitude of the force P that will cause the total length of the member to decrease by 0.25 mm. The values of the elastic modulus for steel and aluminium are 2.1 × 105 N/mm2 and 0.7 × 105 N/mm2 respectively. What is the total work done by the force P?
(A) 27.5
(B) 28.5
A 10 mm diameter mild steel bar of length 1.50 metres is stressed by a weight of 120 N dropping freely through 20 mm before commencing to stretch the bar. Find the maximum instantaneous stress and the elongation produced in the bar. (Take E = 2 × 105 N/mm2)
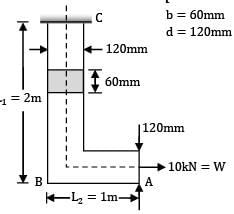
The L-shaped bar shown in the figure is of uniform cross-section 60 mm × 120 mm. Calculate the total strain energy. (Take E = 2 × 105 MPa, G = 0.8 × 105 MPa)



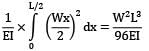
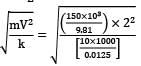
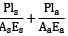 = δ
= δ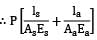 = δ
= δ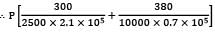 = 0.25mm
= 0.25mm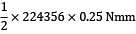
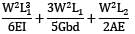
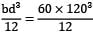 =8.64 × 106 mm4
=8.64 × 106 mm4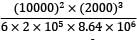 +
+ 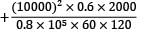 +
+