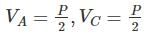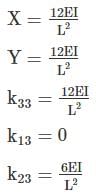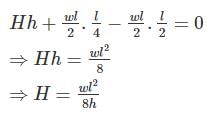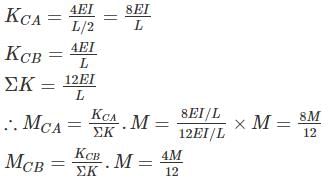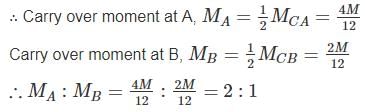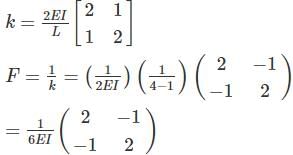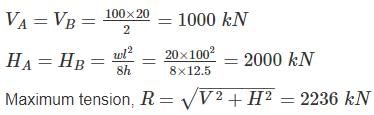Test: Structural Analysis- 3
10 Questions MCQ Test GATE Civil Engineering (CE) 2023 Mock Test Series | Test: Structural Analysis- 3
| 1 Crore+ students have signed up on EduRev. Have you? |
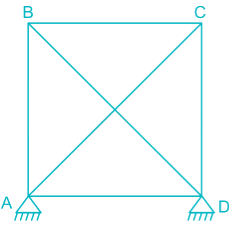
While fabricating a square truss, the member BD was somehow defectively short (fabrication defect) as shown in the figure. So stress developed in the member AC immediately after constructing the truss by force would be
At joint B, FBC → Compressive
At joitnt C, FCA → Tensile
For a linear elastic frame, if the stiffness matrix is doubled with respect to the existing stiffness matrix, the deflection of the resulting frame will be
Stiffness (k) is defined as the force per unit deflection.
K = P/δ
⇒ δ = P/K
If stiffness matrix is doubled
i.e. K’ = 2K
then,
δ = P/K'
δ = P/2K
δ = (1/2)P/K
δ’ = δ/2.
Therefore, if the stiffness matrix is doubled with respect to the existing stiffness matrix, the deflection of the resulting frame will be half the existing value.
At joint C, there is no horizontal reaction,
So, FBC=0,
Due to Loading Symmetricity,
Va = Vc = P
∴ Vc = P/2
∴ FCD = P/2
Now at joint E,
∑Falong the line BE = 0
FBE = P KN
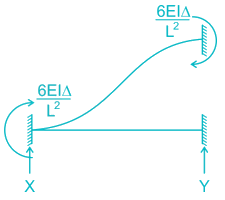
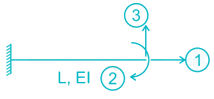
Stiffness coefficient k23 for the beam shown below is
For k33 Apply unit displacement along 3 and restraining the displacement in 2 and 1
Δ → unity
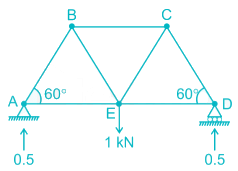
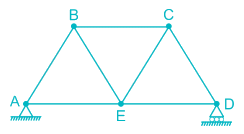
Length of each member of the truss shown in the figure is 3m. Member AB and CD are subjected to a temperature rise of 40°C and coefficient of thermal expansion, α is 12 × 10-6/°C. The vertical deflection at joint E is________
To find the vertical deflection at joint E, a unit vertical load is applied at joint E and the forces in member AB and CD are to be found out.
Consider joint A,
FAB sin 60° = 0.5
FAB = 0.577 (compressive)
Similarly, FCD = 0.577 (compressive)
due to increase in temperature, the increase in length of AB & CD = L ∝ t
= 3 × 12 × 10-6 × 40
= 0.00144 m
So the deflection of joint E,
δ = Σ kδ’
where, k = Force produced in each member when a unit downward load is applied at joint E.
δ’ = Deflection produced in the concerned member (AB & CD) due to temparature rise.
= (- 0.577) × (0.00144) + (- 0.577) × (0.00144)
= - 0.00166 m
= 1.66 mm (upward)
[‘–’ means our assumed downward deflection is wrong, it will deflect upward]
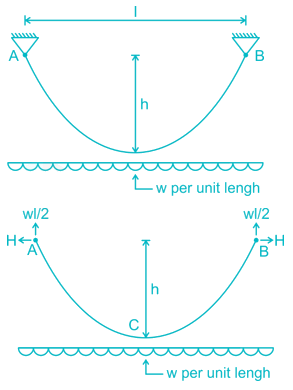
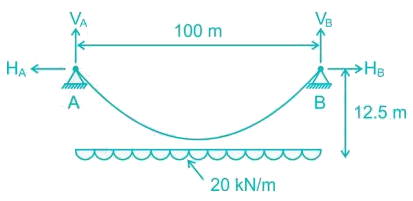
Uniformly distributed load w per unit length is suspended from a cable between point A and B. If the points A and B are at the same level at distance 'l' and central sage of the cable is h, the horizontal thrust developed of supports is -
Taking moment about C,
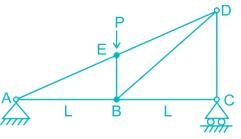
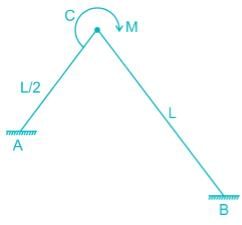
Find the ration of the support moments, MA : MB (flexural rigidity is constant)
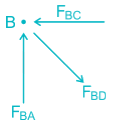
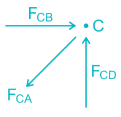
A plane truss is shown below
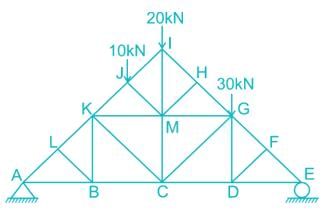
The members who do not carry any force are:
I. Member LK, LA and LB are meeting at joint ‘L’ and AL and LK re co-linear so force in the member LB is zero.
FLB = 0
II. Member FG, FE, and FD are meeting at joint F, So force in the member FD = 0
FFD = 0
III. Removing Member LB, DF, thus member BK, BC and BA meets at point B out of which BA and BC are co-linear and vice versa for member DG, DC and DE.
So, FBK = 0
FDG = 0
IV. Similarly, Member HM, HI and HG are meeting at joint H
FHM = 0
The stiffness matrix of a beam element is
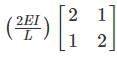
Which one of the following is its flexibility matrix?
A cable carrying a load of 20 kN/m run of the horizontal span, is structured at supports 100 m apart. The supports are at the same level and the central dip is 12.5 m. Find the least tension in the cable.
Minimum tension occurs at deepest point and is equal to horizontal thrust.
Tmin = H = 2000 kN
|
26 docs|292 tests
|
|
Use Code STAYHOME200 and get INR 200 additional OFF
|
Use Coupon Code |
|
26 docs|292 tests
|
Download free EduRev App
Related content with Test: Structural Analysis- 3
|
|
|
Related tests with Test: Structural Analysis- 3
|
|
|
|
|
|
© EduRev
|
Education Revolution
|
Follow Us
|
