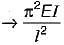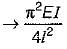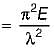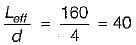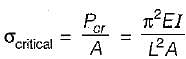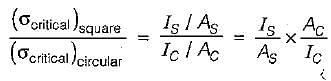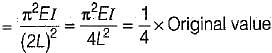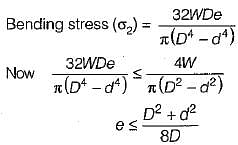Test: Struts & Columns - 3 | 10 Questions MCQ Test

Continue with Google

Continue with Facebook

I accept the Terms & Conditions.

Description

This mock test of Test: Struts & Columns - 3 for Mechanical Engineering helps you for every Mechanical Engineering entrance exam. This contains 10 Multiple Choice Questions for Mechanical Engineering Test: Struts & Columns - 3 (mcq) to study with solutions a complete question bank. The solved questions answers in this Test: Struts & Columns - 3 quiz give you a good mix of easy questions and tough questions. Mechanical Engineering students definitely take this Test: Struts & Columns - 3 exercise for a better result in the exam. You can find other Test: Struts & Columns - 3 extra questions, long questions & short questions for Mechanical Engineering on EduRev as well by searching above.

QUESTION: 1

Compression members always tend to buckle in the direction of the

A.
axis of load
B.
perpendicular to the axis of load
C.
minimum cross-section
D.
least radius of gyration

Solution:

QUESTION: 2

Euler’s formula gives 5 to 10% error in crippling load as compared to experimental results in practice because

A.
effect of direct stress is neglected
B.
pin joints are not free from friction
C.
the assumptions made in using the formula are not met in practice
D.
the material does not behave in an ideal elastic way in tension and compression

Solution:

QUESTION: 3

Match List-I (Long column) with List-ll (Critical Load) and select the correct answer using the codes given below the lists:
List-I
A. Both ends hinged
B. One end fixed and other end free
C. Both ends fixed
D. One end fixed and other end hinged
List-II
1. π² EI/4L²
2. 4π² EI/4L²
3. 2π² EI/4L²
4. π² EI/L²
Codes:
A B C D
(a) 2 1 4 3
(b) 4 1 2 3
(c) 2 3 4 1
(d) 4 3 2 1

A.
(a)
B.
(b)
C.
(c)
D.
(d)

Solution:

(i) Both ends hinged
(ii) One end fixed and other end free
(iii) Both ends fixed
(iv) One end fixed and other end hinged

QUESTION: 4

Given that
P_E = the crippling load given by Euler
P_c= the load at failure due to direct compression
P_R = the load in accordance with the Rankine’s criterion of failure
Then P_R is given by

A.
B.
C.
D.
None of these

Solution:

QUESTION: 5

If the crushing stress in the material of a mild steel column is 3300 kg/cm². Euler’s formula for crippling load is applicable for slenderness ratio equal to/greater than

A.
40
B.
50
C.
60
D.
80

Solution:

For Euler’s formula to be applicable the critical stress must not exceed the proportional limit.
Now crushing stress in mild steel
= 3300 kg/cm²
= 330 N/mm²
But stress at proportional limit in mild steel
= 250 M/mm²
Euler’s buckling stress

λ = 88.55 ≈ 89
Thus slenderness ratio should be more than or equal to 89 ideally. Option (d) is the most close one.

QUESTION: 6

For a circular column having its ends hinged, the slenderness ratio is 160. The L/d ratio of the column is

A.
80
B.
57
C.
40
D.
20

Solution:

Slenderness ratio,
where r is the least radius of gyration and L_eff is effective length

∴

QUESTION: 7

When a column is subjected to an eccentric load, the stress induced in the column will be

A.
direct stress only
B.
bending stress only
C.
shear stress only
D.
direct and bending stress both

Solution:

QUESTION: 8

An aluminium column of square cross-section (10 mm x 10 mm) and length 300 mm has both ends pinned. This is replaced by a circular cross-section (of diameter 10 mm) column of the same length and made of the same material with the same end conditions. The ratio of critical stresses for these two columns corresponding to Euler ’s critical load (σ_critical) square : (σ_critical)circular is

A.
1 : 4
B.
3 : 4
C.
4 : 3
D.
4 : 1

Solution:

For same material, same end condition and same length

QUESTION: 9

If one end of a hinged column is made fixed and the other free, how much is the critical load compared to the original value?

A.
One-fourth
B.
One-half
C.
Twice
D.
Four times

Solution:

Original load =
when one end of hinged column is fixed and other free. New L_θ = 2L
∴ New load

QUESTION: 10

A short column of external diameter D and internal diameter d carries and eccentric load W. The greatest eccentricity which the load can be applied without producing tension on the cross-section of the column would be