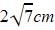Test: Tangents to a Circle - Class 10 MCQ
25 Questions MCQ Test - Test: Tangents to a Circle
In the figure, the pair of tangents AP and AQ, drawn from an external point A to a circle with centre O, are perpendicular to each other and length of each tangent is 4 cm, then the radius of the circle is
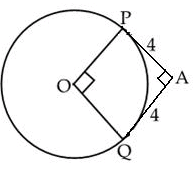
The length of the tangent drawn from a point 8 cm away from the centre of a circle, of radius 6 cm, is :
Number of tangents, that can be drawn to a circle, parallel to a given chord is
How many tangents can be drawn to a circle from a point in its interior?
The tangents drawn at the ends of a diameter of a circle are:
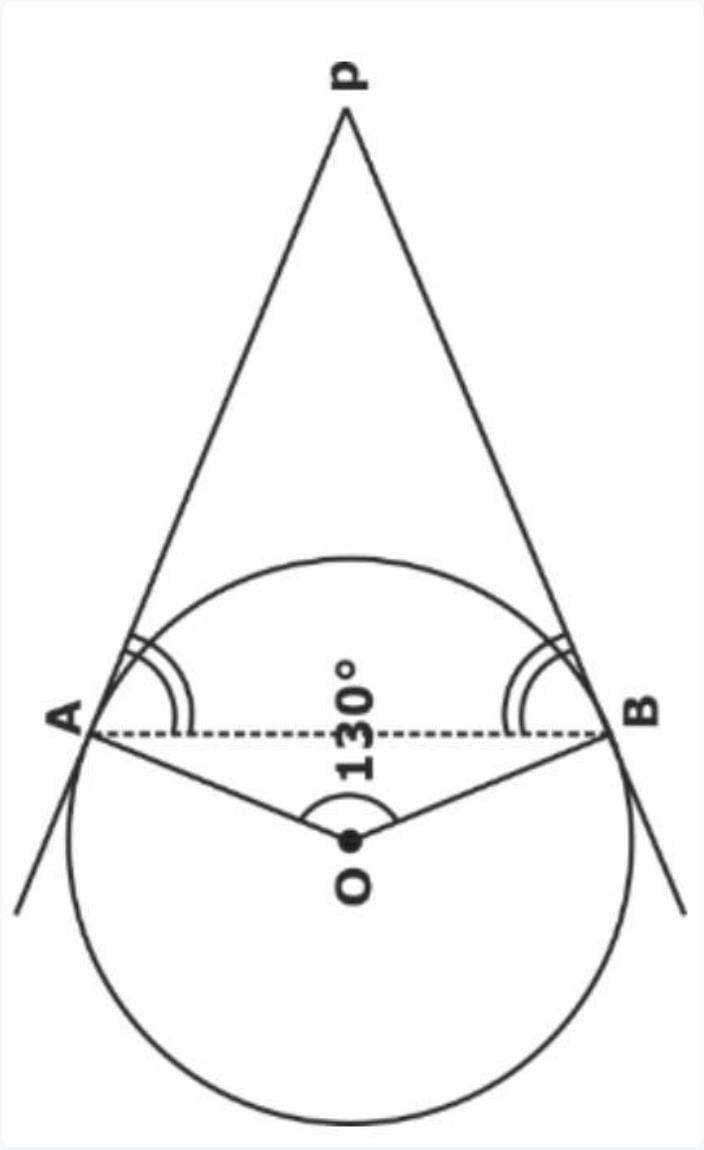
In the given figure, PA and PB are tangents from P to a circle with centre O. If ∠AOB = 130°, then find ∠APB.
From a point A, the length of a tangent to a circle is 8cm and distance of A from the circle is 10cm. The length of the diameter of the circle is
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR =120o, then find ∠OPQ.
If figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P. If ∠POQ = 70o, then ∠TPQ is equal to
A line that intersects a circle in exactly one point is called a
A line that intersects a circle in two distinct points is called a
The length of tangent drawn from an external point P to a circle, with centre O, is 8 cm. If the radius of the circle is 6 cm, then the length of OP (in cm) is:
A line segment having its end points on the circle is called a
Number of tangents from a point lying inside the circle is
The angle between two tangents drawn from an external point to a circle is 110°. The angle subtended at the centre by the segments joining the points of contact to the centre of circle is:
A tangent PA is drawn from an external point P to a circle of radius 3√2 cm such that the distance of the point P from O is 6 cm as shown figure. The value of ∠APO is
What is the distance between two parallel tangents of a circle of the radius 4 cm?
In fig., two concentric circles of radii a and b (a > b) are given. The chord AB of larger circle touches the smaller circle at C. The length of AB is:
A tangent to a circle is a line that intersects the circle in
In the figure, if from an external point T, TP and TQ are two tangents to a circle with centre O so that POQ = 110°, then, PTQ is:
In fig., two circles with centres A and B touch each other externally at k. The length of PQ (in cm) is
The distance between two parallel tangents to a circle of radius 5 cm is
In fig., PA is a tangent to a circle of radius 6 cm and PA = 8 cm, then length of PB is