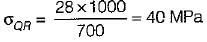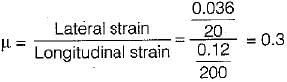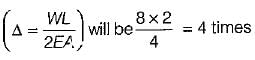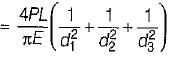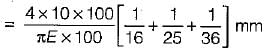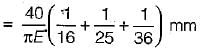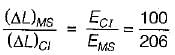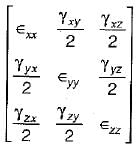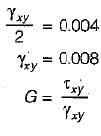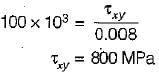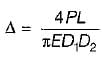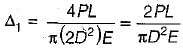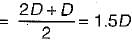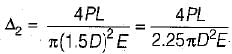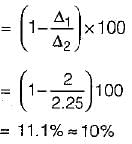Test: Tension, Compression & Shear - 3 - Mechanical Engineering MCQ
10 Questions MCQ Test Topicwise Question Bank for Mechanical Engineering - Test: Tension, Compression & Shear - 3
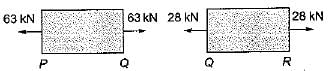
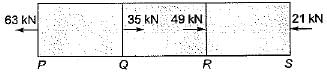
A bar having a cross-sectional area of 700 mm2 is subjected to axial loads at the positions indicated. The value of stress in the segment QR is
A bar of 20 mm diameter is tested in tension. It is observed that when a load of 30 kN is applied the extension measured over a gauge length of 200 mm is 0.12 mm and contraction in diameter is 0.0036 mm. The Poisson’s ratio is
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
If all the dimensions of a prismatic bar of square cross-section suspended freely from the ceiling of a roof are doubled then the total’elongation produced by its own weight will increase
A round bar made of same material consists of 3 parts each of 100 mm length having diameters of 40 mm, 50 mm and 60 mm, respectively, if the bar is subjected to an axial load of 10 kN, the total elongation of the bar in mm would be (E is the modulus of elasticity in kN/mm2)
Two identical circular rods of same diameter and same length are subjected to same magnitude of axial tensile force. One of the rods is made out of mild steel having the modulus of elasticity of 206 GPa. The other rod is made out of cast iron having the modulus of elasticity of 100 GPa. Assume both the materials to be homogeneous and isotropic and the axial force causes the same amount of uniform stress in both the rods. The stresses developed are with in the proportional limit of the respective materials. Which of the following observations is correct?
A uniform, slender cylindrical rod is made of a homogeneous and isotropic material. The rod rests on a frictionless surface. The rod is heated uniformly. If the radial and longitudinal thermal stresses are represented by σr and σz respectively, then
A brass bar of solid section is encased in a steel tube as shown in the diagram below:
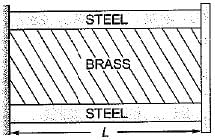
The coefficient of expansion of steel is 11.2 x 10-6 per °C and the coefficient of expansion of brass is 16.5 x 10-6 per °C. The composite bar is heated through 60°C. Now consider the following statements:
1. The stress in brass will be tensile.
2. The stress in steel will be tensile.
3. The stress in steel will be compressive.
4. The stress in brass will be compressive.
Q. Which of these statements are correct?
A uniform bar lying in the x - direction is subjected to pure bending. Which one of the following tensors represents the strain variation when bending moment is about the z-axis (p, q and r constants)?
Assuming E = 160 GPa and G = 100 GPa for a material a strain tensor is given as
The shear stress, τxy is
A bar of circular cross-section varies uniformly from a cross-section 2D to D. If extension of the bar is calculated treating it as a bar of average diameter, then the percentage error will be
|
45 videos|314 tests
|
|
45 videos|314 tests
|
Top Courses for Mechanical Engineering
Important Questions for Tension, Compression & Shear - 3
Tension, Compression & Shear - 3 MCQs with Answers
Online Tests for Tension, Compression & Shear - 3 Topicwise Question Bank for Mechanical Engineering
|
© EduRev
|
Education Revolution
|
Follow Us
|
