Test: Theoretical Distributions- 5

Probability function is known as

The no. of points obtained in a single throw of an unbiased die follow :

The no of points in a single throw of an unbiased die has frequency function

In uniform distribution random variable x assumes n values with

In a discrete random variable x follows uniform distribution and assumes only the values 8 , 9, 11, 15, 18, 20. Then P(x = 9) is

In a discrete random variable x follows uniform distribution and assumes only the values 8 , 9, 11, 15, 18, 20. Then P(x = 12) is

In a discrete random variable x follows uniform distribution and assumes only the values 8, 9, 11, 15, 18, 20. Then P(x < 15) is

In a discrete random variable x follows uniform distribution and assumes only the values 8 , 9, 11, 15, 18, 20. Then P 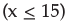 is

In a discrete random variable x follows uniform distribution and assumes only the values 8, 9, 11, 15, 18, 20. Then P(x > 15) is

In a discrete random variable x follows uniform distribution and assumes only the values 8, 9, 11, 15, 18, 20. Then P(|x – 14| < 5) is

When f(x)= 1/n then mean is

In continuous probability distribution P  means

In continuous probability distribution F(x) is called.

The probability density function of a continuous random variable is y = k(x–1),  then the value of the constant k is

 When f(x) = 1/n then mean is 

 In continuous probability distribution P(x ≤ t) means 

 In a discrete random variable x follows uniform distribution and assumes only the values 8, 9, 11, 15, 18, 20. Then P( x > 15) is 

In a discrete random variable x follows uniform distribution and assumes only the values 8, 9, 11, 15, 18, 20. Then P (x ≤ 15) is 

The probability function of a continuous random variable is y = k ( x - 1), (1 ≤ x ≤ 2) then the value of the constant k is 

The no of points in a single throw of an unbiased die has frequency function 

 In a discrete random variable x follows uniform distribution and assumes only the values 8, 9, 11, 15, 18, 20. Then P(|x - 14| < 5) is 

In a discrete random variable x follows uniform distribution and assumes only the values 8, 9, 11, 15, 18, 20. Then P( = 9) is 

The number of points obtained in a single throw of an unbiased die follows:

In uniform distribution random variable x assumes n values with 

Out of 128 families with 4 children each, how many are expected to have at least one boy and one girl?

 If a Poisson distribution is fitted to the following data:

Then the sum of the expected frequencies for x = 0, 1 and 2 is

 If the weekly of 5000 workers in a factory follows normal distribution with mean and SD as Rs.700 and Rs.50 respectively, what is the expected number of workers with wages between Rs.660 and Rs.720?

 A car hire firm has 2 cars which is hired out everyday. The number of demands per day for a car follows Poisson distribution with mean 1.20. What is the proportion of days on which some demand is refused?(Given e ^1.20 = 3.32).

The salary of workers of a factory is known to follow normal distribution with an average salary of Rs.10,000 and standard deviation of salary as Rs.2,000. If 50 workers receiver salary more than Rs.14,000, then the total no. of workers in the factory is 

The number of accidents in a year attributed to taxi drivers in a locality follows Poisson distribution with an average 2. Out of 500 taxi drivers of that area, what is the number of drivers with at least 3 accidents in a year?

 If a random variable X follows binomial distribution with mean as 5 and satisfying the condition 10P(X = 0) =P (X = 1), what is the value of P (x ≥ 1/ x > 0)?

X is a Poisson variate satisfying the following condition 9 P ( x = 4) + 90 P ( x = 6) = P (X = 2 ). What is the value of P (X = 1)? 

In a sample of 800 students, the mean weight and standard deviation of weight are found to be 50 kg and 20 kg respectively. On the assumption of normally, what is the number of students weighing between 46 Kg and 62 Kg? Given area of the standard normal curve between z = 0 to z 0.20 = 0.0793 and area between z = 0 to z = 0.60 = 0.2257.

For a standard normal variate, the value of mean is? 

For a normal distribution with mean as 500 and SD as 120, what is the value of k so that the interval [500, k] covers 40.32 per cent area of the normal curve? Given Φ (1.30) = 0.9032.

In 10 independent rollings of a biased die, the probability that an even number will appear 5 times is twice the probability that an even number will appear 4 times. What is the probability that an even number will appear twice when the die is rolled 8 times?

 A renowned hospital usually admits 200 patients every day. One per cent patients , on an average, require special room facilities. On one particular morning, it was found that only one special room is available. What is the probability that more than 3 patients would require special room facilities?