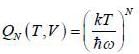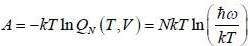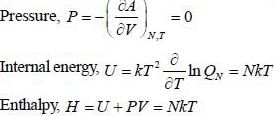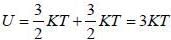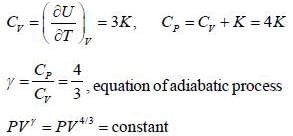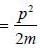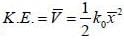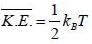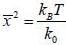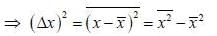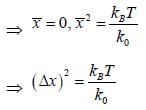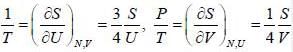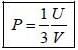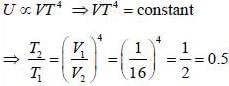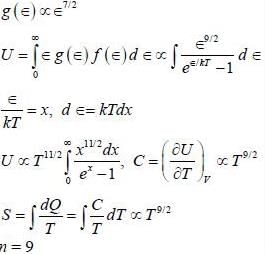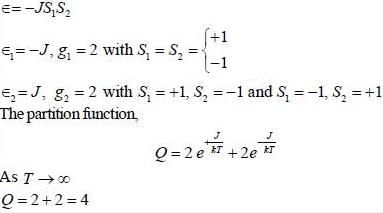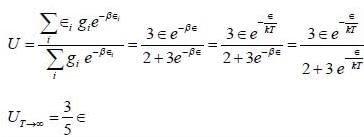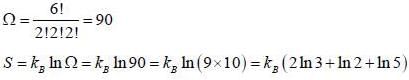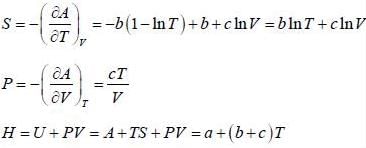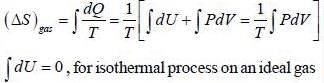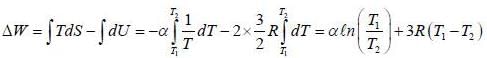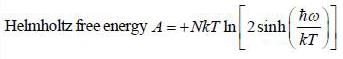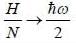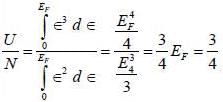Test: Thermo And Statistical - 1 - Physics MCQ
20 Questions MCQ Test GATE Physics Mock Test Series 2025 - Test: Thermo And Statistical - 1
Consider a system of N non-interacting classical linear harmonic oscillates (each of mass m and angular frequency ω) in thermal equilibrium at temperature T. The enthalpy of the system is
The equation of state for adiabatic process performed on an ideal gas consisting of non-relativistic rigid triangular molecule in terms of pressure (P) and volume (V) is given by
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Consider a sensitive spring balance characterized by a spring constant k0. The balance is in an environment whose temperature is T. A small object of mass m is suspended to the spring. The mean fluctuation in its position is
The entropy (S) of a thermodynamics system is give in terms of its internal energy (U) and volume (V) by S= C U^(3/4) V^(1/4) , where c is constant.
The pressure (P) of the system is given by
Which of the following can exhibit Bose-Einstein condensation, even in principle?
Two gases are separated by an impermeable but movable and conducting partition in an isolated container. Both gases are in which type of equilibrium?
Which option is not correct for a liquid to vapour phase transition at critical point?
One mole of an ideal gas at 300K expands reversibly and isothermally from a pressure of 1.5 x 103 N/m2 to 5 x 102 N/m2. The change in entropy (J/K) of the universe is _____________.
Consider a photon gas inside a 3-D cavity of volume V and in thermal equilibrium at temperature T. If photon gas is expanded adiabatically into vacuum to 16 times of initial volume, then its temperaure changes to n times of initial tempeature. The value of n is _________________.
Six distinghuishable particles are distributed over three non-degenerate levels of energies 0, ∈ and 2∈. The energy of most probable macrostate of the system is _______ ∈.
A branch of excitations for a 3-dimension system has a dispersion relation, ∈(k) = A k2/3 where, A is constant, ∈ is energy' and k is the magnitude of wave vector. The excitations are bosonic in nature and chemical potential is zero. The entropy(S) of the system varies on absolute temperature (T) as S ∝ Tn/2, the value of n is
The entropy of a system of N spins, which may align either in the upward or in the downward direction. The probability of upward directions is 1/3 and that of downward direction is 2/3. The entropy per spin in unit of kB is _______
Consider a system of two ising spin S1 and S2 taking value ±1 with interaction energy ∈ = -JS1S2 in thermal equilibrium at temperature T. The partition function of the system in the limit T → ∞ is ______.
Consider a system that has two energy' levels of energy 0 and ∈. The lowest level is doubly degenerate while excited level is triply degenerate. The system is in thermal equilibrium at temperature T. The average energy of the system in very high temperature limit is
What is the maximum entropy of the system when six distinguishable particles are distributed over three non-degenerate energy states of energies 0, ∈ and 2 ∈ ?
The Helmholtz free energy (A) of atherm odynam ic system in terms of volum e (V) and temperature (T) is given by
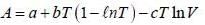
where a. b and c are constants The enthalpy (H) of the system is
One mole of an ideal gas at 27°C expands reversibly and isothermally from a pressure of 2 x 106 N/m2 to a pressure 2 x 105 N/m2 The change in entropy (in J/K) of the gas is
A process is performed on 2 moles of an ideal mono-atomic gas in which its entropy depends an absolute temperature T as S = α/T, where α is a constant. What is the work performed by the eas if its temperature varies from T1 to T2?
For a system of non-interacting one-dimension quantum oscillators of angular frequency ω, the value of enthalpy in ther limit per oscillator T → 0, is
Consider an ideal gas of NFemnons inside a 3-D container of volume V. Assume that the dispersion relation ∈ (k) x ∝, the ratio of the ground state energy per particle to the Fermi energy at absolute zero of temperature is
|
1 docs|34 tests
|