All Courses
Get the App Signup / Login
Sign in Open App
Electrical Engineering (EE) Exam  >  Electrical Engineering (EE) Tests  >  Test: Time Response Of Second Order Systems - 1 - Electrical Engineering (EE) MCQ

Test: Time Response Of Second Order Systems - 1 - Electrical Engineering (EE) MCQ


Test Description

10 Questions MCQ Test - Test: Time Response Of Second Order Systems - 1

Test: Time Response Of Second Order Systems - 1 for Electrical Engineering (EE) 2024 is part of Electrical Engineering (EE) preparation. The Test: Time Response Of Second Order Systems - 1 questions and answers have been prepared according to the Electrical Engineering (EE) exam syllabus.The Test: Time Response Of Second Order Systems - 1 MCQs are made for Electrical Engineering (EE) 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Time Response Of Second Order Systems - 1 below.
Solutions of Test: Time Response Of Second Order Systems - 1 questions in English are available as part of our course for Electrical Engineering (EE) & Test: Time Response Of Second Order Systems - 1 solutions in Hindi for Electrical Engineering (EE) course. Download more important topics, notes, lectures and mock test series for Electrical Engineering (EE) Exam by signing up for free. Attempt Test: Time Response Of Second Order Systems - 1 | 10 questions in 10 minutes | Mock test for Electrical Engineering (EE) preparation | Free important questions MCQ to study for Electrical Engineering (EE) Exam | Download free PDF with solutions
Test: Time Response Of Second Order Systems - 1 - Question 1
Save

Which of the following transfer function will have the greatest maximum overshoot? 

Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 1

Answer: d
Explanation: Comparing the characteristic equation with the standard equation the value of the damping factor is calculated and the value for the option d is minimum hence the system will have the maximum overshoot .

Test: Time Response Of Second Order Systems - 1 - Question 2
Save

A system generated by

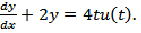
The ramp component in the forced response will be:

Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 2

Answer: b
Explanation:

Laplace transforming
sY(s) + 2Y(s)=4/s2
Taking the inverse Laplace transform the forced term is 2t u(t).

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Time Response Of Second Order Systems - 1 - Question 3
Save

The system in originally critically damped if the gain is doubled the system will be :

Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 3

Answer: c
Explanation:

hence due to this G lies between 0 and 1.

Test: Time Response Of Second Order Systems - 1 - Question 4
Save

Let c(t) be the unit step response of a system with transfer function K(s+a)/(s+K). If c(0+) = 2 and c(∞) = 10, then the values of a and K are respectively.
Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 4

Answer: c
Explanation: Applying initial value theorem which state that the initial value of the system is at time t =0 and this is used to find the value of K and final value theorem to find the value of a.

Test: Time Response Of Second Order Systems - 1 - Question 5
Save

The damping ratio and peak overshoot are measures of:
Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 5

Answer: b
Explanation: Speed of response is the speed at which the response takes the final value and this is determined by damping factor which reduces the oscillations and peak overshoot as the peak is less then the speed of response will be more.

Test: Time Response Of Second Order Systems - 1 - Question 6
Save

Find the type and order of the system given below:
Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 6

Answer: Type = 2 which is the number of poles at the origin and order is the highest power of the characteristic equation.

Test: Time Response Of Second Order Systems - 1 - Question 7
Save

A system has a complex conjugate root pair of multiplicity two or more in its characteristic equation. The impulse response of the system will be:
Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 7

Answer: c
Explanation: Poles are the roots of the denominator of the transfer function and on imaginary axis makes the system stable but multiple poles makes the system unstable.

Test: Time Response Of Second Order Systems - 1 - Question 8
Save

The forward path transfer function is given by G(s) = 2/s(s+3). Obtain an expression for unit step response of the system. 
Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 8

Answer: d
Explanation: C(s)/R(s) = s/(s2+3s+2)
C(s) = 1/s-2/s+1+1/s+2
c(t) = 1-2e-t+e+2t.

Test: Time Response Of Second Order Systems - 1 - Question 9
Save

Find the initial and final values of the following function:

F(s) = 12(s+1)/s(s+2)^2(s+3)
Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 9

Answer: d
Explanation: Using final and initial values theorem directly to find initial and final values but keeping in mind that final value theorem is applicable for stable systems only.

Test: Time Response Of Second Order Systems - 1 - Question 10
Save

The step response of the system is c(t) = 10+8e-t-4/8e-2t . The gain in time constant form of transfer function will be: 
Detailed Solution for Test: Time Response Of Second Order Systems - 1 - Question 10

Answer: d
Explanation: Differentiating the equation and getting the impulse response and then taking the inverse Laplace transform and converting the form into time constant form we get K = -7.5.

Information about Test: Time Response Of Second Order Systems - 1 Page
In this test you can find the Exam questions for Test: Time Response Of Second Order Systems - 1 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Time Response Of Second Order Systems - 1, EduRev gives you an ample number of Online tests for practice

Top Courses for Electrical Engineering (EE)

Download as PDF

Top Courses for Electrical Engineering (EE)

Important Questions for Time Response Of Second Order Systems - 1

Find all the important questions for Time Response Of Second Order Systems - 1 at EduRev.Get fully prepared for Time Response Of Second Order Systems - 1 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Time Response Of Second Order Systems - 1 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Time Response Of Second Order Systems - 1 resources.

Time Response Of Second Order Systems - 1 MCQs with Answers

Prepare for the Time Response Of Second Order Systems - 1 within the Electrical Engineering (EE) exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Time Response Of Second Order Systems - 1

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Time Response Of Second Order Systems - 1 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Follow Us
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup