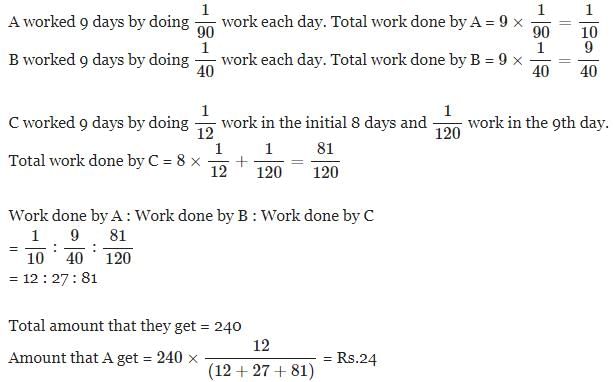Test: Time & Work (March 5) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - Test: Time & Work (March 5)
Refer to the data below and answer the questions that follow.
Anoop was writing the reading comprehension sections in Lhe DOG entrance examinations, There were four passages of exactly equal length in terms of number of words and die four passages had 5, 8, 8 and 6 questions following each of them respectively. It is known that Anoop can answer exactly 12 questions in the time he takes to read any one of the four passages. Assume that his rate of reading and answering questions remains the same throughout the section.
Q.
By what per cent should Anoop increase his reading speed if he has to cut down on his total time spent on the section by 20%? Assume that the time spent on answering the questions is constant and as given in the directions.
A can do a piece of work in 90 days, B in 40 days and C in 12 days. They work for a day each in turn, i.e., first day A does it alone, second day B does it alone and 3rd day C does it alone. After that the cycle is repeated till the work is finished. They get Rs 240 for this job. If the wages are divided in proportion to the work each had done. Find the amount A will get?
There are three taps A, B and C in a tank. They can fill the tank in 25 hrs, 20 hrs and 10 hrs respectively. At first all of them are opened simultaneously. Then after 1 hrs, tap C is closed and tap A and B are kept running. After the 4th hour, tap B is also closed. The remaining work is done by tap A alone.
Find the percentage of work done by tap A itself?
Find the percentage of work done by tap A itself?
Anup can dig a well in 10 days. but particularly in difficult time the work is such that due to fatigue every subsequent day efficiency of a worker falls by 10%.If Anup is given a task of digging one such well in the difficult time, then in how many days will he finish the work?
Mayank can do 50% more work than Shishu in the same time. Shishu alone can do a piece of work in 30 hours. Shishu starts working and he had already worked for 12 hours when Mayank joins him. How many hours should Shishu and Mayank work together to complete the remaining work?
In what time would a cistern be filled by three pipes of diameter of 1 cm, 2 cm and 3 cm if the largest pipe alone can fill the cistern in 49 minutes, the amount of water flowing through each pipe being proportional to the square of its diameter?
A and B together can complete a work in 3 days. They start together but after 2 days, B left the work. If the work is completed after two more days, B alone could do the work in
A can work twice as fast as B. A and C together can work thrice as fast as B. If A, B and C complete a job in 30 days working together, in how many days can each of them complete the work?
Read the passage below and solve the questions based on it.
The tank at a water supply station is filled with water by several pumps. At first three pumps of Ihe same capacity are turned on: 2.5 hours later, two more pumps (both the same) of a different capacity are set into operation. After 1 hour, the additional pumps were set into operation; the tank was almost filled to its capacity (15 m3 were still lacking): in another hour the tank was full. One of the two additional pumps could have filled the tank in 40 hours
Q. What is the volume of the tank?
Read the passage below and solve the questions based on it.
There are three taps A, B and C and an outlet pipe D. A, B and C can fill the tank in the Panikam locality in 10, 20 and 25 h respectively. The outlet pipe can empty the same tank in 100 h. There are 2,000 houses in the locality. The tank has a capacity of 50,000 litres
Q.
If all the taps and the outlet pipe are opened simultaneously, how much water is thrown into the tank every hour?
|
152 docs|327 tests
|


 .
.