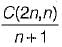All Courses
Get the App Signup / Login
Sign in Open App
Computer Science Engineering (CSE) Exam  >  Computer Science Engineering (CSE) Tests  >  Question Bank for GATE Computer Science Engineering  >  Test: Trees- 2 - Computer Science Engineering (CSE) MCQ

Test: Trees- 2 - Computer Science Engineering (CSE) MCQ


Test Description

15 Questions MCQ Test Question Bank for GATE Computer Science Engineering - Test: Trees- 2

Test: Trees- 2 for Computer Science Engineering (CSE) 2024 is part of Question Bank for GATE Computer Science Engineering preparation. The Test: Trees- 2 questions and answers have been prepared according to the Computer Science Engineering (CSE) exam syllabus.The Test: Trees- 2 MCQs are made for Computer Science Engineering (CSE) 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Trees- 2 below.
Solutions of Test: Trees- 2 questions in English are available as part of our Question Bank for GATE Computer Science Engineering for Computer Science Engineering (CSE) & Test: Trees- 2 solutions in Hindi for Question Bank for GATE Computer Science Engineering course. Download more important topics, notes, lectures and mock test series for Computer Science Engineering (CSE) Exam by signing up for free. Attempt Test: Trees- 2 | 15 questions in 45 minutes | Mock test for Computer Science Engineering (CSE) preparation | Free important questions MCQ to study Question Bank for GATE Computer Science Engineering for Computer Science Engineering (CSE) Exam | Download free PDF with solutions
Test: Trees- 2 - Question 1
Save

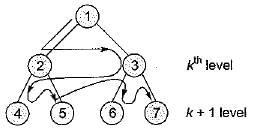
Level order traversal of a rooted tree can be done by starting from the root and performing

Detailed Solution for Test: Trees- 2 - Question 1

Level order traversal of rooted tree can be done by starting from root and visiting all node at k level before visiting any node at k + 1 level, which is nothing but breadth first search.

Test: Trees- 2 - Question 2
Save

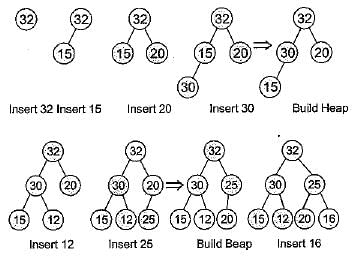
The elements 32, 15, 20, 30, 12, 25, 16 are inserted one by one in the given order into a maxHeap. The resultant maxHeap is

Detailed Solution for Test: Trees- 2 - Question 2

Input sequence 32,15, 20, 30,12, 25,16 If i is the root then A [i] > A [2i] for 1 < i < n/2 and A [i] > A [2i + 1] for 1 < i < n/2 where 2i is the left of i and 2i + 1 is the right of i of a max heap.

1 Crore+ students have signed up on EduRev. Have you? Download the App
Test: Trees- 2 - Question 3
Save

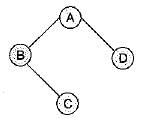
Which one of the following binary trees has its inorder and preorder traversals as BCAD and ABCD, respectively?

Detailed Solution for Test: Trees- 2 - Question 3


Inorder traversal is BCAD and preorder traversal is ABCD.

Test: Trees- 2 - Question 4
Save

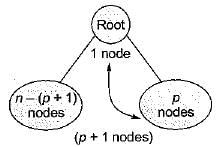
The numbers 1 , 2 .... n are inserted in a binary search tree in some order, In the resulting tree, the right subtree of the root contains p nodes. The first number to be inserted in the tree must be
Detailed Solution for Test: Trees- 2 - Question 4

Number 1 ,2 , 3, ....... n are inserted into BST in some order.

Since we know total nodes = n
So, Left (root) + 1 + p = n
Left (root) = n - p - 1
Left (root) = n - (p + 1)
So, root element will be = left element + 1
= n - (p + 1) + 1
= n - p - 1 + 1
= n - p

Test: Trees- 2 - Question 5
Save

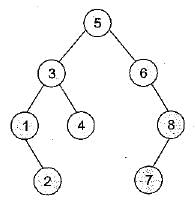
A binary search tree contains the numbers 1,2, 3, 4, 5, 6, 7, 8, When the tree is traversed in preorder and the values in each node printed out, the sequence of values obtained is 5, 3,1, 2, 4, 6, 8, 7. If the tree is traversed in postorder, the sequence obtained would be
Detailed Solution for Test: Trees- 2 - Question 5

Test: Trees- 2 - Question 6
Save

How many distinct binary search trees can be created out of 4 distinct keys?
Detailed Solution for Test: Trees- 2 - Question 6

Total number of distinct binary search tree with n nodes (key)

Test: Trees- 2 - Question 7
Save

In a complete k-ary, every internal node has exactly k children. The number of leaves in such a tree with n internal nodes is
Detailed Solution for Test: Trees- 2 - Question 7

In a complete-k-ary tree. If every internal node has exacity k children then (k - 1) key contains no leaves, if there are n internal nodes, then number of leaves is n(k- 1) + 1.

Test: Trees- 2 - Question 8
Save

In a binary max heap containing.n numbers, the smallest element can be found in time
Detailed Solution for Test: Trees- 2 - Question 8

MAX Heap used to identity max element in O(1) time for to identity min element require O(n), to apply the linear search.

Test: Trees- 2 - Question 9
Save

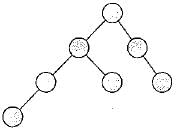
In a binary tree, the number of internal nodes of degree 1 is 5, and the number of internal nodes of degree 2 is 10. The number of leaf nodes in the binary tree is
Detailed Solution for Test: Trees- 2 - Question 9

Let number of vertices in binary tree = n Number of edges = n - 1
So, n - 1 = 1 x 5 + 2 x 10
n - 1 = 5 + 20
n = 26
Num ber of leaf nodes = 26 - 5 - 10 = 11

Test: Trees- 2 - Question 10
Save

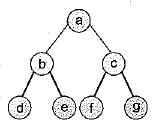
The inorder and preorder traversal of a binary tree are “dbeafcg" and “abdecfg’’ respectively. The postorder traversal of the binary tree is
Detailed Solution for Test: Trees- 2 - Question 10

The in order traversal sequence is dbeafcg and the pre order traversal sequence is abdecfg.
So the tree is

In the post order traversal the sequence is debfgca.

Test: Trees- 2 - Question 11
Save

Consider the process of inserting an element into a Max Heap, where the Max Heap is represented by an array. Suppose we perform a binary search on the path from the new leaf to the root to find the position for the newly inserted element, the number of comparisons performed is
Detailed Solution for Test: Trees- 2 - Question 11

After inserting an element at leaf in max heap we perform binary search on the path from the new leaf to the root to find the correct position for the newly inserted element. Comparisions will take θ(loglogn) but time will be θ(logn) because of swap operations.

Test: Trees- 2 - Question 12
Save

How many distinct BSTs can be constructed with 3 distinct keys?
Detailed Solution for Test: Trees- 2 - Question 12

For distinct BST we apply this formula 

n = 3 here so C(6, 3) = 20 and 20/4 = 5

Test: Trees- 2 - Question 13
Save

What is the maximum height of any AVL-tree with 7 nodes? Assume that the height of a tree with a single node is 0.
Detailed Solution for Test: Trees- 2 - Question 13

Maximum height of any AVL-tree with 7.

(There may be different way to draw AVL with 7 nodes).

Test: Trees- 2 - Question 14
Save

A max-heap is a heap where the value of each parent is greater than or equal to the value of its children. Which of the following is a max-heap?
Detailed Solution for Test: Trees- 2 - Question 14

Test: Trees- 2 - Question 15
Save

We are given a set of n distinct elements and an unlabeled binary tree with n nodes. In how many ways can we populate the tree with the given set so that it becomes a binary search tree?
Detailed Solution for Test: Trees- 2 - Question 15

63 videos|8 docs|165 tests
Join Course
Information about Test: Trees- 2 Page
In this test you can find the Exam questions for Test: Trees- 2 solved & explained in the simplest way possible. Besides giving Questions and answers for Test: Trees- 2, EduRev gives you an ample number of Online tests for practice

Top Courses for Computer Science Engineering (CSE)

Download as PDF

Top Courses for Computer Science Engineering (CSE)

Important Questions for Trees- 2

Find all the important questions for Trees- 2 at EduRev.Get fully prepared for Trees- 2 with EduRev's comprehensive question bank and test resources. Our platform offers a diverse range of question papers covering various topics within the Trees- 2 syllabus. Whether you need to review specific subjects or assess your overall readiness, EduRev has you covered. The questions are designed to challenge you and help you gain confidence in tackling the actual exam. Maximize your chances of success by utilizing EduRev's extensive collection of Trees- 2 resources.

Trees- 2 MCQs with Answers

Prepare for the Trees- 2 within the Computer Science Engineering (CSE) exam with comprehensive MCQs and answers at EduRev. Our platform offers a wide range of practice papers, question papers, and mock tests to familiarize you with the exam pattern and syllabus. Access the best books, study materials, and notes curated by toppers to enhance your preparation. Stay updated with the exam date and receive expert preparation tips and paper analysis. Visit EduRev's official website today and access a wealth of videos and coaching resources to excel in your exam.

Online Tests for Trees- 2 Question Bank for GATE Computer Science Engineering

Practice with a wide array of question papers that follow the exam pattern and syllabus. Our platform offers a user-friendly interface, allowing you to track your progress and identify areas for improvement. Access detailed solutions and explanations for each test to enhance your understanding of concepts. With EduRev's Online Tests, you can build confidence, boost your performance, and ace Trees- 2 with ease. Join thousands of successful students who have benefited from our trusted online resources.
© EduRev
Education Revolution
Signup to see your scores go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup