Test: Triangles- 2 - GRE MCQ
20 Questions MCQ Test - Test: Triangles- 2
In ΔLMN, LM = |x-7|, MN = |x-4| and NL = x + 1, where x is a number whose value is not known. Is ΔLMN an acute triangle (a triangle each of whose angles measures less than 90∘)?
(1) NM = 10
(2) LM = 7
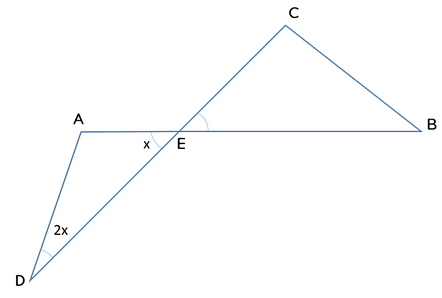
Triangles AED and BEC are formed using the straight lines AB and CD as shown in the figure above. If BE = BC, DE2 > AD2 + AE2 and the measure of ∠AED is x, which of the following statements must be true?
- CE2 > 2BE2
- AE < AD
- DE < CE
The figure above shows a triangle ABC in which the measure of ∠ABC, b∘is greater than 90∘
If AB = 3 units and BC = 4 units, which of the following can be the measure of side AC?
- 6
- 7
- 8
The figure above shows the position, at two instants of time, of a 10-meter-long rod as it was falling down to the ground. If one end of the rod was pinned to the ground, by what vertical distance did the rod fall between the two instants of time?
Triangle ABC is an isosceles triangle with AB = AC and AD is the perpendicular dropped from vertex A on the side BC. What is the perimeter of triangle ABC?
(1) ∠BAD = 2∠ACD
(2) The perimeter of triangle ADB is 15 + 5√3
The figure above shows two right triangles ΔPSR and ΔPRQ that share a common side PR, which measures 5 units. If QR = 4PS, what is the area of the quadrilateral PQRS?
(1) The area of ΔPSR is 6 square units
(2) The area of ΔPRQ is 30 square units
Triangle ABC is inscribed in a rectangle ABEF forming two right triangles: AFC and BEC. Is triangle ABC an equilateral triangle?
In the figure above, triangle ABC is an isosceles triangle with AB = BC and BD is the perpendicular dropped from vertex B to the side AC. Point E is marked on BD such that ∠DAE = 450 and ∠ECB = 150. If the ratio of length CD: BD = 1: √3. What is the ratio of the area of triangle BEC to the area of the triangle ABC?
In the figure above, ΔABC and ΔBCD are right-angled at points B and C respectively. If AC = 3√2, ∠ACB = 45∘ and ∠CBD = 30∘, what is the area of ΔBCD?
In the figure shown above, x is the length of side BD of triangle ABD. If D is a point that lies on line AC and x is an integer, what is the value of x?
In the figure above, Δ POQ and Δ AOB are both right-angled at point O. If BQ = OB and OA = AP, and the length of side AB is 5 units, what is the area of the shaded region?
(1) OA = OB + 1
(2) If a rectangle is drawn with sides of length 2QB and PA /4 the area of the rectangle will be 6 square units
In the above figure, lines AB and CD are perpendicular to one another. If AD is parallel to BC and ∠CAB = 2∠ABD, what is the
measure of ∠ACB?
(1) ∠CAD = 90
(2) ∠ CBD = 60
Sam climbs up a 40/√3 metres long ladder that is inclined at an angle of 60 to the ground. Upon reaching the upper edge of the ladder, he drops a coin to the ground. If the time taken, in seconds, by an object to drop by a height of h meters is equal to , then how much time does the coin dropped by Sam take to reach the ground?
What is the value of a?
(1) The area of an equilateral triangle of side length 3a units is 9√3 square units
(2) The area of an isosceles triangle whose sides are of length 4a, 4a and a units is 3√7 square units
In ΔABC, point D lies on the side AB between vertices A and B.
If CD = CB, is AD > BC?
(1) ∠ADC = 110
(2) ∠ACD = 30
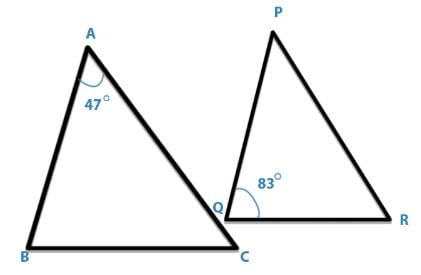
If ABC and PQR are similar triangles in which ∠ A = 470 and ∠ Q = 830, then ∠ C is:
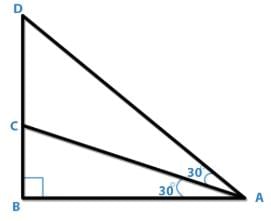
In the following figure which of the following statements is true?
In triangle PQR length of the side QR is less than twice the length of the side PQ by 2 cm. Length of the side PR exceeds the length of the side PQ by 10 cm. The perimeter is 40 cm. The length of the smallest side of the triangle PQR is :