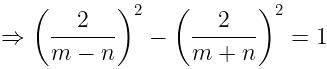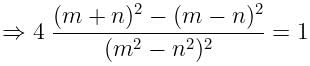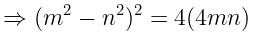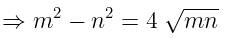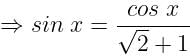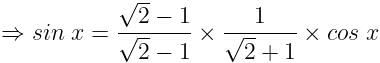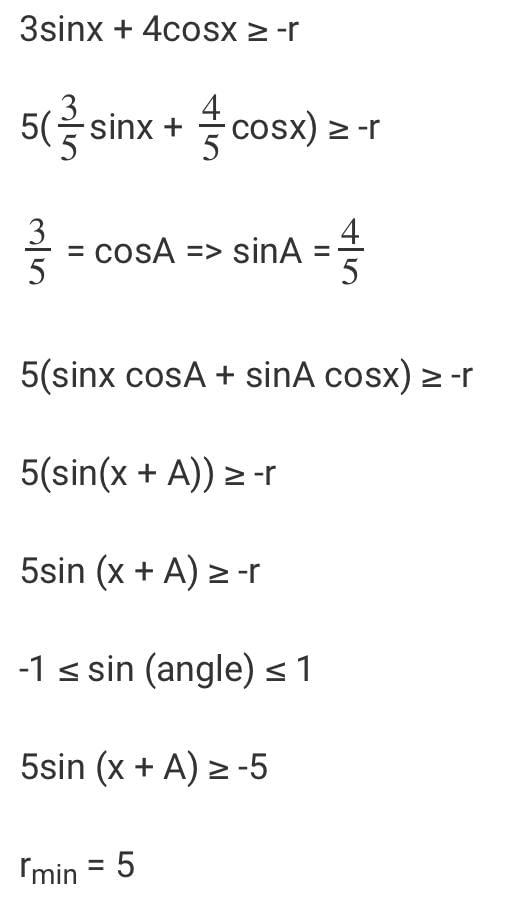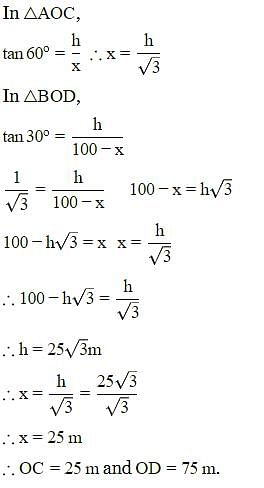Test: Trigonometry- 1 (May 20) - CAT MCQ
10 Questions MCQ Test Daily Test for CAT Preparation - Test: Trigonometry- 1 (May 20)
If tanØ + sinØ = m, tanØ - sinØ = n, find the value of m2 - n2.
A student is standing with a banner at the top of a 100 m high college building. From a point on the ground, the angle of elevation of the top of the student is 60° and from the same point, the angle of elevation of the top of the tower is 45°. Find the height of the student.
If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:
If cos A + cos2 A = 1 and a sin12 A + b sin10 A + c sin8 A + d sin6 A - 1 = 0. Find the value of a+b / c+d
If sin (A + B) = √3 / 2 and tan (A – B) = 1. What are the values of A and B?
3sinx + 4cosx + r is always greater than or equal to 0. What is the smallest value ‘r’ can to take?
A right angled triangle has a height ‘p’, base ‘b’ and hypotenuse ‘h’. Which of the following value can h2 not take, given that p and b are positive integers?
If Cos x – Sin x = √2 Sin x, find the value of Cos x + Sin x:
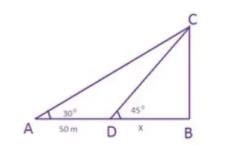
Anil looked up at the top of a lighthouse from his boat and found the angle of elevation to be 30 degrees. After sailing in a straight line 50 m towards the lighthouse, he found that the angle of elevation changed to 45 degrees. Find the height of the lighthouse.
Two poles of equal height are standing opposite to each other on either side of a road which is 100 m wide. Find a point between them on road, angles of elevation of their tops are 30∘ and 60∘. The height of each pole in meter, is:
|
152 docs|327 tests
|