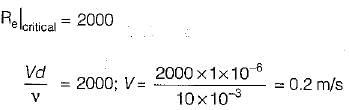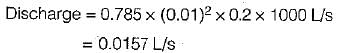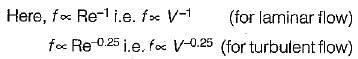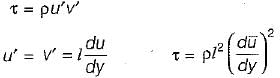Mechanical Engineering Exam > Mechanical Engineering Tests > Fluid Mechanics for Mechanical Engineering > Test: Turbulent Flow - 2 - Mechanical Engineering MCQ
Test: Turbulent Flow - 2 - Mechanical Engineering MCQ
Test Description
9 Questions MCQ Test Fluid Mechanics for Mechanical Engineering - Test: Turbulent Flow - 2
Test: Turbulent Flow - 2 for Mechanical Engineering 2024 is part of Fluid Mechanics for Mechanical Engineering preparation. The Test: Turbulent Flow - 2 questions and answers have been
prepared according to the Mechanical Engineering exam syllabus.The Test: Turbulent Flow - 2 MCQs are made for Mechanical Engineering 2024 Exam. Find important
definitions, questions, notes, meanings, examples, exercises, MCQs and online tests for Test: Turbulent Flow - 2 below.
Solutions of Test: Turbulent Flow - 2 questions in English are available as part of our Fluid Mechanics for Mechanical Engineering for Mechanical Engineering & Test: Turbulent Flow - 2 solutions in
Hindi for Fluid Mechanics for Mechanical Engineering course. Download more important topics, notes, lectures and mock
test series for Mechanical Engineering Exam by signing up for free. Attempt Test: Turbulent Flow - 2 | 9 questions in 30 minutes | Mock test for Mechanical Engineering preparation | Free important questions MCQ to study Fluid Mechanics for Mechanical Engineering for Mechanical Engineering Exam | Download free PDF with solutions
Detailed Solution for Test: Turbulent Flow - 2 - Question 1
Test: Turbulent Flow - 2 - Question 2
Water of kinematic viscosity v = 1 centistoke flows through a 10 mm diameter pipe. The critical flow in this pipe would correspond to a discharge of approximately
Detailed Solution for Test: Turbulent Flow - 2 - Question 2
| 1 Crore+ students have signed up on EduRev. Have you? Download the App |
Detailed Solution for Test: Turbulent Flow - 2 - Question 3
Test: Turbulent Flow - 2 - Question 4
Friction factor f in laminar and turbulent flow in a pipe varies as Re-1 and Re-0.25 respectively. If V\s the average velocity, the pressure drop in a horizontal pipe for laminar and turbulent flow respectively will be proportional to
Detailed Solution for Test: Turbulent Flow - 2 - Question 4
Test: Turbulent Flow - 2 - Question 6
The critical value of reynolds number for transition from laminar to turbulent boundary layer in external flows is taken as
Detailed Solution for Test: Turbulent Flow - 2 - Question 6
Detailed Solution for Test: Turbulent Flow - 2 - Question 7
Test: Turbulent Flow - 2 - Question 8
In a fully turbulent flow through a rough pipe, the friction factor ‘f’ is (Re is Reynolds number and ξs/D is relative roughness)
Test: Turbulent Flow - 2 - Question 9
Using the Prandtl's mixing length concept, how is the turbulent shear stress expressed?
Detailed Solution for Test: Turbulent Flow - 2 - Question 9
|
56 videos|104 docs|75 tests
|
Information about Test: Turbulent Flow - 2 Page
In this test you can find the Exam questions for Test: Turbulent Flow - 2 solved & explained in the simplest way possible.
Besides giving Questions and answers for Test: Turbulent Flow - 2, EduRev gives you an ample number of Online tests for practice
|
56 videos|104 docs|75 tests
|
Download as PDF


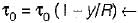 shear stress variation where y is distance from pipe wall, so, the shear stress varies linearly with the distance from the boundary to become zero at the center.
shear stress variation where y is distance from pipe wall, so, the shear stress varies linearly with the distance from the boundary to become zero at the center.