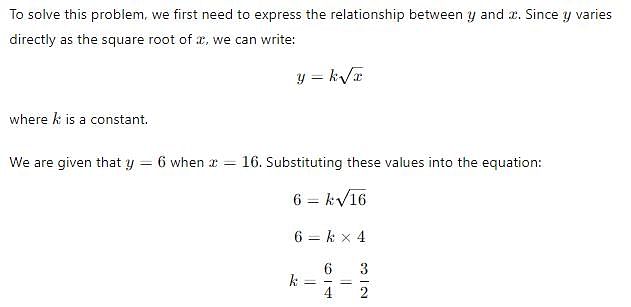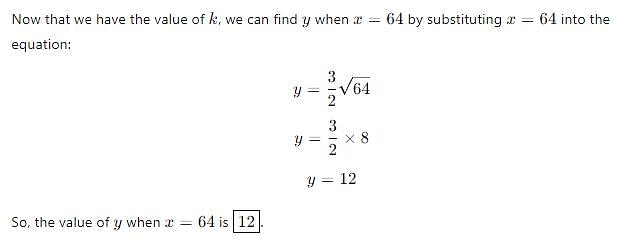Test: Variation - 1 - JAMB MCQ
10 Questions MCQ Test Mathematics for JAMB - Test: Variation - 1
If y varies directly as x, and y = 10 when x = 5, what is the value of y when x = 8?
If a varies inversely as b, and a = 4 when b = 6, what is the value of b when a = 9?
If y varies directly as the square root of x, and y = 6 when x = 16, what is the value of y when x = 64?
If y varies inversely as the cube of x, and y = 10 when x = 2, what is the value of y when x = 4?
If y varies directly as x and inversely as z, and y = 6 when x = 3 and z = 4, what is the value of y when x = 6 and z = 8?
If y varies directly as the square of x, and y = 25 when x = 5, what is the value of y when x = 10?
If y varies inversely as the cube root of x, and y = 12 when x = 64, what is the value of y when x = 8?
If y varies directly as the square root of x, and y = 2 when x = 25, what is the value of y when x = 100?
If y varies inversely as x, and y = 6 when x = 3, what is the value of y when x = 5?
If y varies directly as x and inversely as the square of z, and y = 12 when x = 4 and z = 2, what is the value of y when x = 6 and z = 3?
|
139 videos|82 docs|101 tests
|